CF1389E Calendar Ambiguity

伯兰德历法一年有 $m$ 个月，每个月有 $d$ 天。月份编号从 $1$ 到 $m$。伯兰德一周有 $w$ 天。一年的第一天也是一周的第一天。注意，最后一周可能少于 $w$ 天。 如果一对 $(x, y)$ 满足 $x < y$，并且第 $y$ 月的第 $x$ 天与第 $x$ 月的第 $y$ 天是同一周的同一天，则称该对为“模糊对”。 请计算有多少对“模糊对”。

第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。 接下来的 $t$ 行，每行包含三个整数 $m$、$d$ 和 $w$（$1 \le m, d, w \le 10^9$），分别表示一年中的月份数、每月的天数和每周的天数。

输出 $t$ 个整数，每个测试用例输出一行，表示满足条件的 $(x, y)$ 对的数量。

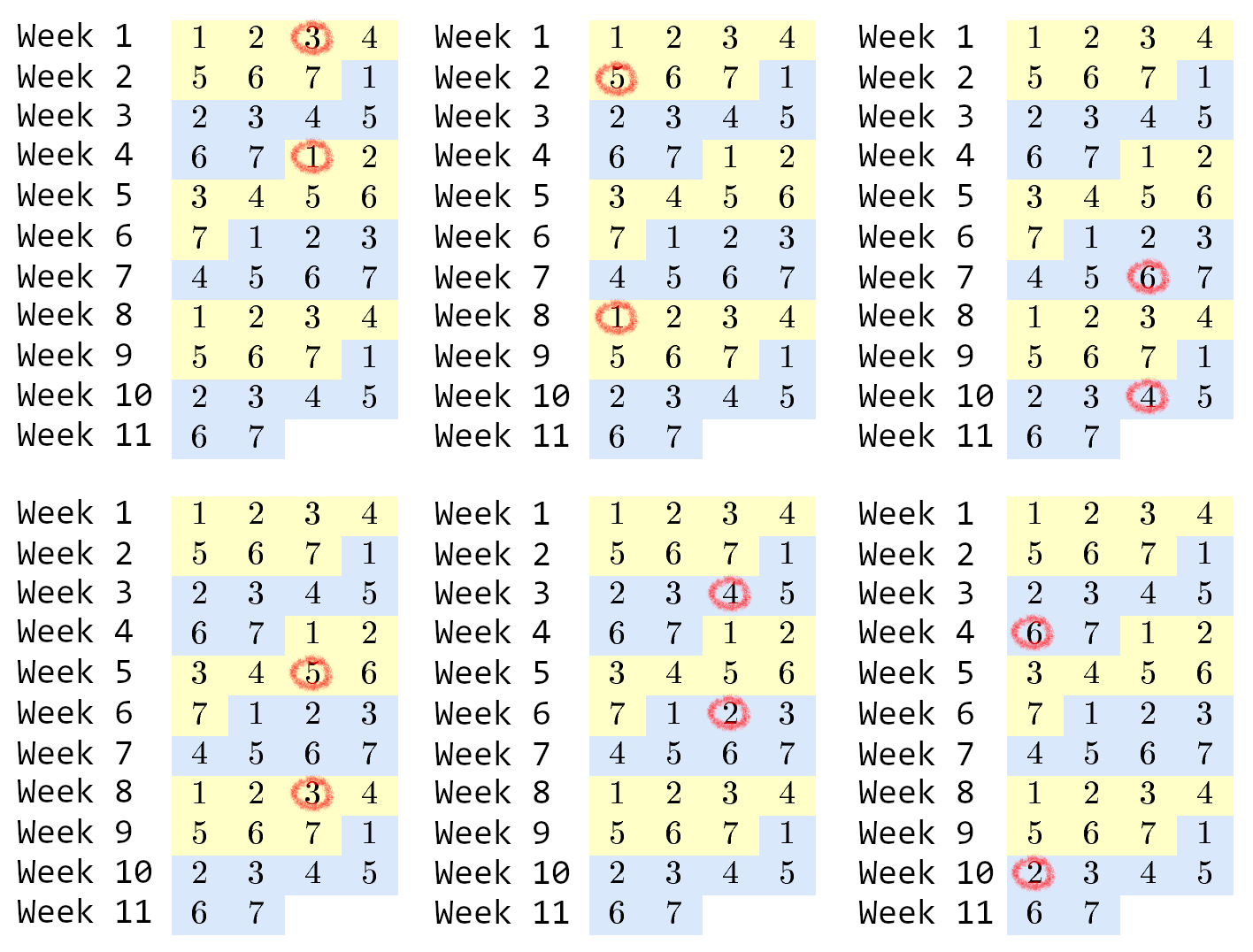
以下是第一个测试用例的所有“模糊对”：  由 ChatGPT 4.1 翻译