CF1394B Boboniu Walks on Graph

Boboniu有一条n个点和m条边的有向图 每个点的出度最大为k 每一条边都有一个权值，没有两条边有相同的权值。 Boboniu喜欢在图上以某种特定的方式走路，这个方式可以表示为特定的集合$(c_1,c_2,\dots,c_k)$。如果他现在在的点的初度为$i$，那么他会走到u的出边中权值第$c_i$小的边 现在bobiniu要你计算所有满足下列条件的边数： - 对于任意的i（$1 \leq i \leq k$），$1 \leq c_i \leq i$ - 对于任意的点u，按上述方式都可以走回自己

第一行有三个数n,m,k$(2 \leq n \leq 2*10^5,2 \leq m \leq min(2*10^5,n*(n-1)),1 \leq k \leq 9)$ 接下来有m行，每行三个数u,v,w$(1 \leq u,v \leq n,u \neq v,1 \leq w \leq m)$，表示一条从u到v的边。保证没有自环和重边。保证所有点都至少有1条出边 保证所有点出度最多为k，保证没有两条边权值相同

一个数：环的个数

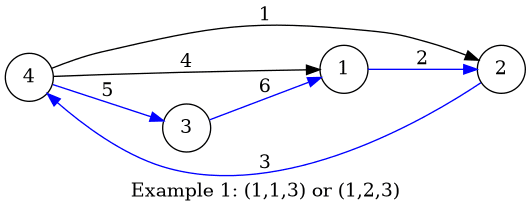
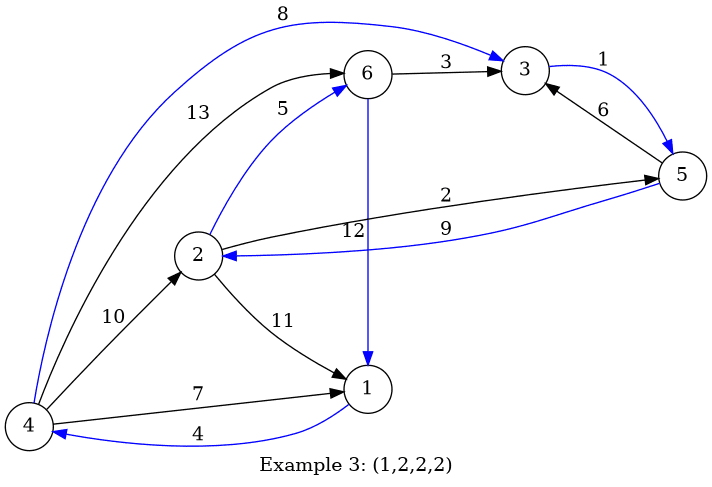
样例1有两种方案：(1,1,3)和(1,2,3)，图中蓝的边是boboniu决定走的边  样例3只有一种方案：(1,2,2,2)  点的出度表示从这个点出去的边的条数