CF1394D Boboniu and Jianghu

自从 Boboniu 建立了他的江湖后，他每天都在这些山上练习功夫。 Boboniu 为他的 $n$ 座山设计了一张地图。他用 $n-1$ 条道路将所有 $n$ 座山连接起来。任意两座山之间都可以通过道路连通。 对于第 $i$ 座山，Boboniu 估算在山顶练功的疲劳度为 $t_i$。他还估算了每座山的高度 $h_i$。 一条路径是一个山峰序列 $M$，满足对于每个 $i$（$1 \le i < |M|$），$M_i$ 和 $M_{i+1}$ 之间有一条道路。Boboniu 会将一条路径视为一次挑战，如果对于每个 $i$（$1 \le i < |M|$），都有 $h_{M_i} \le h_{M_{i+1}}$。 Boboniu 想要将所有 $n-1$ 条道路划分为若干次挑战。注意，每条道路必须且只能出现在一次挑战中，但一座山可以出现在多次挑战中。 Boboniu 希望使完成所有挑战的总疲劳度最小。一次挑战 $M$ 的疲劳度为该路径上所有山的疲劳度之和，即 $\sum_{i=1}^{|M|} t_{M_i}$。 他请你帮他计算最小的总疲劳度。作为回报，你将成为他江湖中的守护者。

第一行包含一个整数 $n$（$2 \le n \le 2 \cdot 10^5$），表示山的数量。 第二行包含 $n$ 个整数 $t_1, t_2, \ldots, t_n$（$1 \le t_i \le 10^6$），表示在每座山顶练功的疲劳度。 第三行包含 $n$ 个整数 $h_1, h_2, \ldots, h_n$（$1 \le h_i \le 10^6$），表示每座山的高度。 接下来的 $n-1$ 行，每行包含两个整数 $u_i, v_i$（$1 \le u_i, v_i \le n, u_i \neq v_i$），表示一条道路连接的两座山。保证所有山通过道路连通。

输出一个整数：所有挑战的最小总疲劳度。

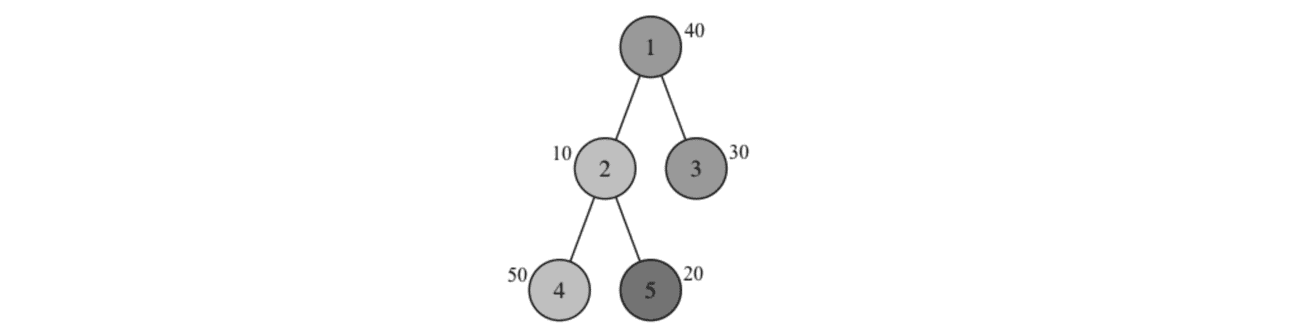
对于第一个样例：  在图中，点越亮表示山越高。最优划分之一为： - 挑战 $1$：$3 \to 1 \to 2$ - 挑战 $2$：$5 \to 2 \to 4$ Boboniu 的总疲劳度为 $(30 + 40 + 10) + (20 + 10 + 50) = 160$。可以证明这是最小的总疲劳度。 由 ChatGPT 4.1 翻译