CF1394E Boboniu and Banknote Collection

No matter what trouble you're in, don't be afraid, but face it with a smile. I've made another billion dollars! — Boboniu Boboniu has issued his currencies, named Bobo Yuan. Bobo Yuan (BBY) is a series of currencies. Boboniu gives each of them a positive integer identifier, such as BBY-1, BBY-2, etc. Boboniu has a BBY collection. His collection looks like a sequence. For example: We can use sequence $ a=[1,2,3,3,2,1,4,4,1] $ of length $ n=9 $ to denote it. Now Boboniu wants to fold his collection. 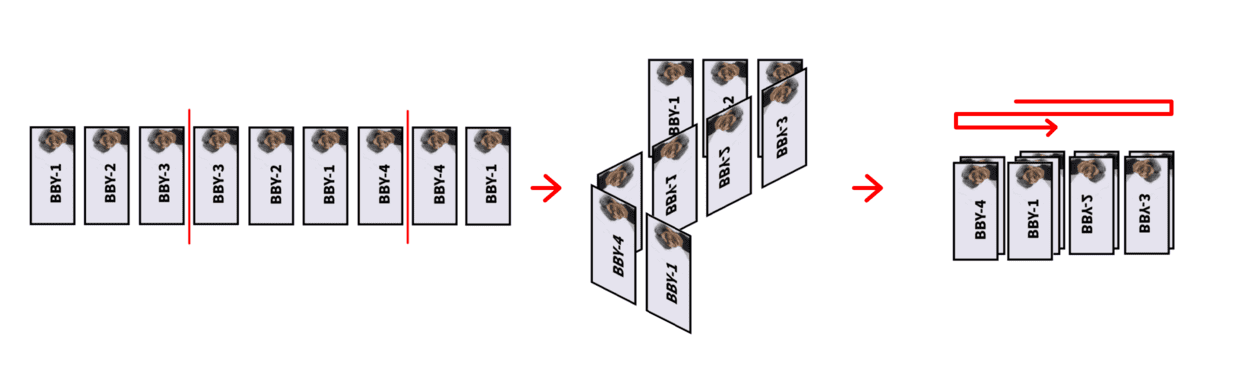You can imagine that Boboniu stick his collection to a long piece of paper and fold it between currencies: Boboniu will only fold the same identifier of currencies together. In other words, if $ a_i $ is folded over $ a_j $ ( $ 1\le i,j\le n $ ), then $ a_i=a_j $ must hold. Boboniu doesn't care if you follow this rule in the process of folding. But once it is finished, the rule should be obeyed. A formal definition of fold is described in notes. According to the picture above, you can fold $ a $ two times. In fact, you can fold $ a=[1,2,3,3,2,1,4,4,1] $ at most two times. So the maximum number of folds of it is $ 2 $ . As an international fan of Boboniu, you're asked to calculate the maximum number of folds. You're given a sequence $ a $ of length $ n $ , for each $ i $ ( $ 1\le i\le n $ ), you need to calculate the maximum number of folds of $ [a_1,a_2,\ldots,a_i] $ .

The first line contains an integer $ n $ ( $ 1\le n\le 10^5 $ ). The second line contains $ n $ integers $ a_1,a_2,\ldots,a_n $ ( $ 1\le a_i\le n $ ).

Print $ n $ integers. The $ i $ -th of them should be equal to the maximum number of folds of $ [a_1,a_2,\ldots,a_i] $ .

Formally, for a sequence $ a $ of length $ n $ , let's define the folding sequence as a sequence $ b $ of length $ n $ such that: - $ b_i $ ( $ 1\le i\le n $ ) is either $ 1 $ or $ -1 $ . - Let $ p(i)=[b_i=1]+\sum_{j=1}^{i-1}b_j $ . For all $ 1\le i