CF1394E Boboniu and Banknote Collection

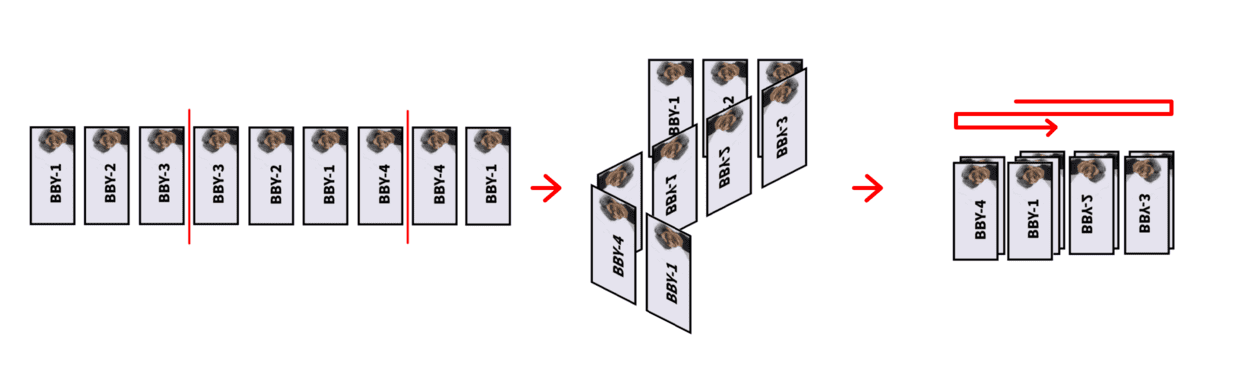
无论遇到什么麻烦，都不要害怕，要微笑着面对。 我又赚了十亿美元！ —— Boboniu Boboniu 发行了自己的货币，名为 Bobo 元。Bobo 元（BBY）是一系列货币。Boboniu 给每种货币分配了一个正整数编号，比如 BBY-1、BBY-2 等。 Boboniu 有一套 BBY 收藏。他的收藏可以看作一个序列。例如：  我们可以用长度为 $n=9$ 的序列 $a=[1,2,3,3,2,1,4,4,1]$ 来表示它。 现在 Boboniu 想要折叠他的收藏。你可以想象 Boboniu 把他的收藏贴在一条长纸条上，然后在货币之间进行折叠：  Boboniu 只会将相同编号的货币折叠在一起。换句话说，如果 $a_i$ 被折叠到 $a_j$ 上（$1\le i,j\le n$），那么必须有 $a_i=a_j$。Boboniu 并不在意你在折叠过程中是否遵守这个规则，但最终结果必须满足这个条件。 折叠的正式定义见下方提示。 根据上图，你最多可以将 $a$ 折叠两次。实际上，对于 $a=[1,2,3,3,2,1,4,4,1]$，最多可以折叠两次。因此，它的最大折叠次数是 $2$。 作为 Boboniu 的国际粉丝，你需要计算最大折叠次数。 给定一个长度为 $n$ 的序列 $a$，对于每个 $i$（$1\le i\le n$），你需要计算 $[a_1,a_2,\ldots,a_i]$ 的最大折叠次数。

第一行包含一个整数 $n$（$1\le n\le 10^5$）。 第二行包含 $n$ 个整数 $a_1,a_2,\ldots,a_n$（$1\le a_i\le n$）。

输出 $n$ 个整数，第 $i$ 个数表示 $[a_1,a_2,\ldots,a_i]$ 的最大折叠次数。

形式化地，对于长度为 $n$ 的序列 $a$，我们定义折叠序列为长度为 $n$ 的序列 $b$，满足： - $b_i$（$1\le i\le n$）要么为 $1$，要么为 $-1$。 - 令 $p(i)=[b_i=1]+\sum_{j=1}^{i-1}b_j$。对于所有 $1\le i