CF1395B Boboniu Plays Chess
题目描述
Boboniu 喜欢和他的员工下国际象棋。众所周知,没有员工能在棋局中击败老板,因此 Boboniu 从未输过任何一局。
你是他公司的一名新应聘者。Boboniu 将用以下国际象棋问题考察你:
给定一个 $n\times m$ 的棋盘(行编号为 $1$ 到 $n$,列编号为 $1$ 到 $m$)。你有一个棋子,初始位于某个不是边界的格子 $(S_x, S_y)$(即 $2 \le S_x \le n-1$ 且 $2 \le S_y \le m-1$)。
从格子 $(x, y)$ 出发,你可以将棋子移动到 $(x, y')$($1 \le y' \le m,\, y' \neq y$)或 $(x', y)$($1 \le x' \le n,\, x' \neq x$)。换句话说,棋子的移动方式与“车”相同。你可以从当前位置移动到同一行或同一列的任意格子。
你的目标是恰好访问每个格子一次。你能找到一种方案吗?
注意:在两次相邻移动之间经过的路径上的格子不算作访问过,不要求回到起点。
输入格式
输入仅一行,包含四个整数 $n$、$m$、$S_x$ 和 $S_y$($3 \le n, m \le 100$,$2 \le S_x \le n-1$,$2 \le S_y \le m-1$),分别表示行数、列数以及棋子的初始位置。
输出格式
你需要输出 $n \cdot m$ 行。
第 $i$ 行应包含两个整数 $x_i$ 和 $y_i$($1 \leq x_i \leq n$,$1 \leq y_i \leq m$),表示你访问的第 $i$ 个格子。你需要恰好输出 $nm$ 对 $(x_i, y_i)$,且它们覆盖所有可能的 $(x_i, y_i)$,其中 $1 \leq x_i \leq n$,$1 \leq y_i \leq m$。
可以证明,在这些约束下总存在解。如果有多种答案,输出任意一种即可。
说明/提示
以下是两个样例的可能路线:
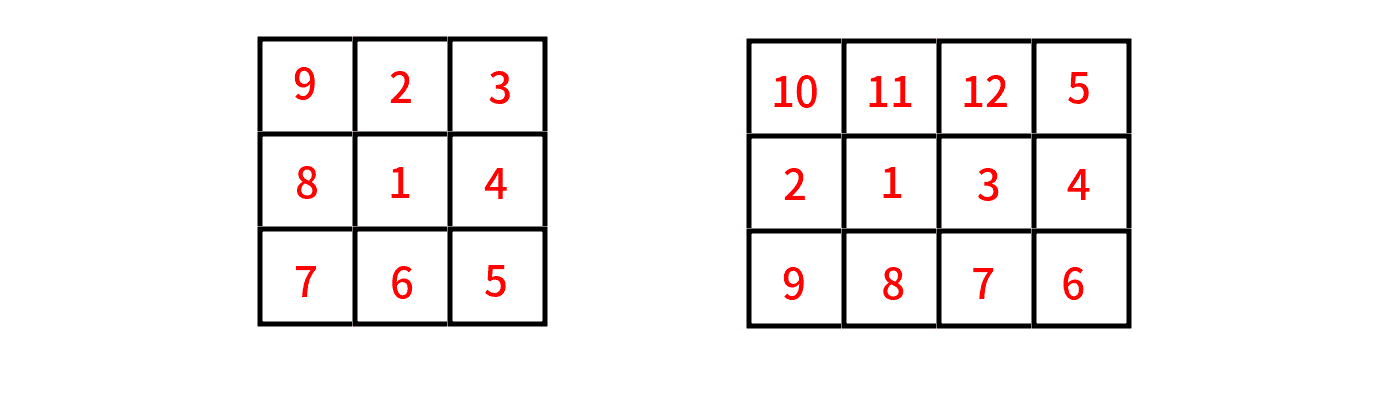
由 ChatGPT 4.1 翻译