CF1396D Rainbow Rectangles

Shrimpy Duc 是一个又胖又贪吃的男孩，总是饿个不停。在寻找食物以满足他永无止境的饥饿感时，Shrimpy Duc 发现了一些无人看管的 M&M 糖果，散落在一个 $L \times L$ 的网格上。网格上共有 $n$ 颗 M&M 糖果，第 $i$ 颗糖果位于 $(x_i + 0.5, y_i + 0.5)$，颜色为 $c_i$，总共有 $k$ 种颜色（M&M 的大小可以忽略不计）。 Shrimpy Duc 想要偷取一个矩形区域内的 M&M 糖果。具体来说，他希望选择一个网格内的整数坐标矩形，并偷取该矩形内的所有糖果。Shrimpy Duc 并不需要偷走所有糖果，但他希望每种颜色至少偷到一颗。 换句话说，他想选择一个边平行于坐标轴的矩形，其左下角顶点为 $(X_1, Y_1)$，右上角顶点为 $(X_2, Y_2)$，且顶点坐标均为整数，满足 $0 \le X_1 < X_2 \le L$ 且 $0 \le Y_1 < Y_2 \le L$，使得对于每种颜色 $1 \le c \le k$，该矩形内至少包含一颗颜色为 $c$ 的 M&M 糖果。 请问有多少个这样的矩形？由于答案可能很大，只需输出答案对 $10^9 + 7$ 取模后的结果。

第一行包含三个正整数 $n, k, L$，分别表示 M&M 糖果的数量、颜色的种类数和网格的边长，满足 $1 \leq k \leq n \leq 2 \cdot 10^3, 1 \leq L \leq 10^9$。 接下来的 $n$ 行描述每颗 M&M 糖果。每行包含三个整数 $x_i, y_i, c_i$，分别表示第 $i$ 颗糖果的坐标和颜色，满足 $0 \leq x_i, y_i < L, 1 \le c_i \le k$。 不同的糖果坐标各不相同（对于任意 $i \ne j$，有 $x_i \ne x_j$ 或 $y_i \ne y_j$），且每种颜色 $1 \le c \le k$ 至少有一颗糖果。

输出一个整数，表示满足条件的矩形数量，对 $10^9 + 7$ 取模。

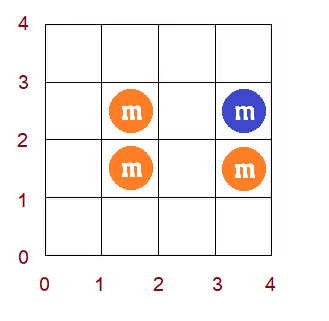
第一个样例的网格如下：  由 ChatGPT 4.1 翻译