CF1398G Running Competition

A running competition is going to be held soon. The stadium where the competition will be held can be represented by several segments on the coordinate plane: - two horizontal segments: one connecting the points $ (0, 0) $ and $ (x, 0) $ , the other connecting the points $ (0, y) $ and $ (x, y) $ ; - $ n + 1 $ vertical segments, numbered from $ 0 $ to $ n $ . The $ i $ -th segment connects the points $ (a_i, 0) $ and $ (a_i, y) $ ; $ 0 = a_0 < a_1 < a_2 < \dots < a_{n - 1} < a_n = x $ . 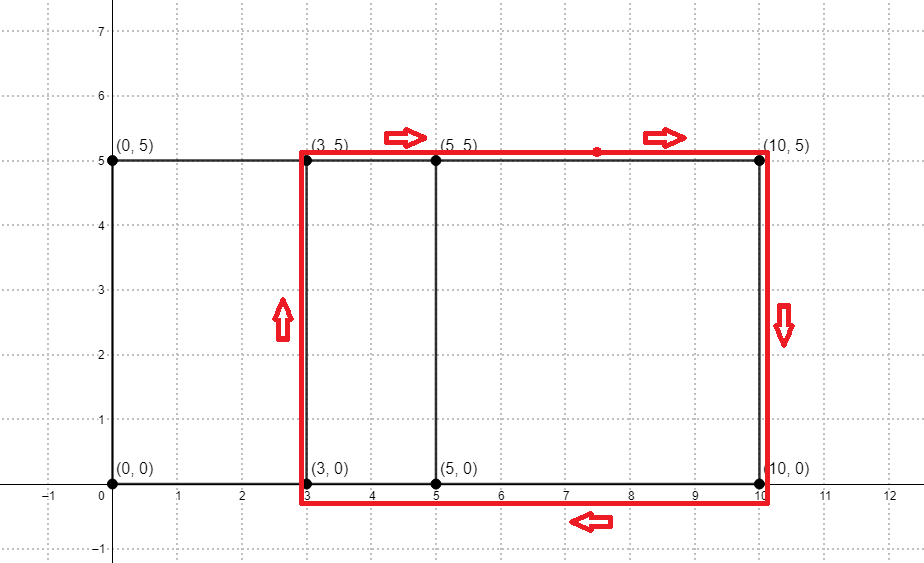For example, here is a picture of the stadium with $ x = 10 $ , $ y = 5 $ , $ n = 3 $ and $ a = [0, 3, 5, 10] $ : A lap is a route that goes along the segments, starts and finishes at the same point, and never intersects itself (the only two points of a lap that coincide are its starting point and ending point). The length of a lap is a total distance travelled around it. For example, the red route in the picture representing the stadium is a lap of length $ 24 $ . The competition will be held in $ q $ stages. The $ i $ -th stage has length $ l_i $ , and the organizers want to choose a lap for each stage such that the length of the lap is a divisor of $ l_i $ . The organizers don't want to choose short laps for the stages, so for each stage, they want to find the maximum possible length of a suitable lap. Help the organizers to calculate the maximum possible lengths of the laps for the stages! In other words, for every $ l_i $ , find the maximum possible integer $ L $ such that $ l_i \bmod L = 0 $ , and there exists a lap of length exactly $ L $ . If it is impossible to choose such a lap then print $ -1 $ .

The first line contains three integers $ n $ , $ x $ and $ y $ ( $ 1 \le n, x, y \le 2 \cdot 10^5 $ , $ n \le x $ ). The second line contains $ n + 1 $ integers $ a_0 $ , $ a_1 $ , ..., $ a_n $ ( $ 0 = a_0 < a_1 < a_2 < \dots < a_{n - 1} < a_n = x $ ). The third line contains one integer $ q $ ( $ 1 \le q \le 2 \cdot 10^5 $ ) — the number of stages. The fourth line contains $ q $ even integers $ l_1 $ , $ l_2 $ , ..., $ l_q $ ( $ 4 \le l_i \le 10^6 $ ) — the lengths of the stages.

Print $ q $ numbers. The $ i $ -th number should be equal to the maximum possible length of a suitable lap for the $ i $ -th stage, or $ -1 $ if it is impossible to choose a lap for that stage.