CF1398G Running Competition

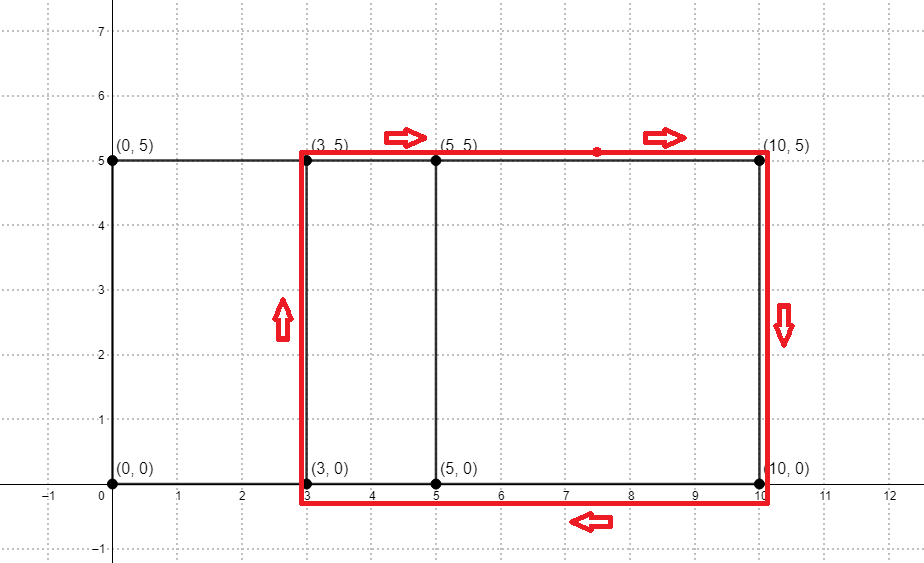
一场跑步比赛即将举行。比赛场地可以用坐标平面上的若干线段表示： - 两条水平线段：一条连接点 $(0, 0)$ 和 $(x, 0)$，另一条连接点 $(0, y)$ 和 $(x, y)$； - $n+1$ 条竖直线段，编号从 $0$ 到 $n$。第 $i$ 条线段连接点 $(a_i, 0)$ 和 $(a_i, y)$，其中 $0 = a_0 < a_1 < a_2 < \dots < a_{n-1} < a_n = x$。 例如，下图展示了 $x = 10$，$y = 5$，$n = 3$，$a = [0, 3, 5, 10]$ 时的场地：  一圈（lap）是沿着这些线段走的路线，起点和终点为同一点，且路线不会自交（唯一重合的点是起点和终点）。一圈的长度是沿路线走过的总距离。例如，图中红色路线是一圈，其长度为 $24$。 比赛将分为 $q$ 个阶段。第 $i$ 个阶段的长度为 $l_i$，组织者希望为每个阶段选择一圈，使得该圈的长度是 $l_i$ 的约数。组织者不希望选择太短的圈，因此对于每个阶段，他们想要找到满足条件的最大可能圈长。 请帮助组织者计算每个阶段最大可能的圈长！换句话说，对于每个 $l_i$，找到最大的整数 $L$，使得 $l_i \bmod L = 0$，且存在长度恰好为 $L$ 的一圈。 如果无法选择这样的圈，则输出 $-1$。

第一行包含三个整数 $n$、$x$ 和 $y$（$1 \le n, x, y \le 2 \times 10^5$，$n \le x$）。 第二行包含 $n+1$ 个整数 $a_0, a_1, \ldots, a_n$（$0 = a_0 < a_1 < a_2 < \dots < a_{n-1} < a_n = x$）。 第三行包含一个整数 $q$（$1 \le q \le 2 \times 10^5$），表示阶段数。 第四行包含 $q$ 个偶数 $l_1, l_2, \ldots, l_q$（$4 \le l_i \le 10^6$），表示每个阶段的长度。

输出 $q$ 个数字。第 $i$ 个数字表示第 $i$ 个阶段满足条件的最大圈长，如果无法选择则输出 $-1$。

由 ChatGPT 4.1 翻译