CF1401A Distance and Axis
题目描述
在 $OX$ 轴上有一个点 $A$,其坐标为 $x = n$。我们希望找到一个整数点 $B$(同样在 $OX$ 轴上),使得从 $O$ 到 $B$ 的距离与从 $A$ 到 $B$ 的距离的绝对差等于 $k$。
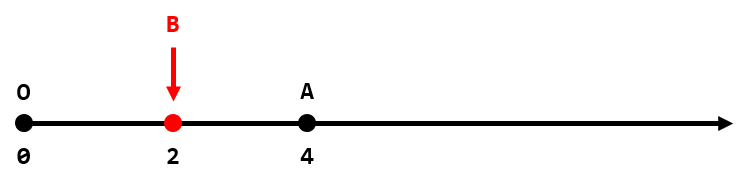 上图为第一个测试用例的描述。由于有时无法找到这样的点 $B$,我们可以每次将 $A$ 的坐标加 $1$ 或减 $1$。请问最少需要多少步,才能使得存在满足条件的点 $B$?
输入格式
第一行包含一个整数 $t$($1 \le t \le 6000$),表示测试用例的数量。
每个测试用例包含一行,包含两个整数 $n$ 和 $k$($0 \le n, k \le 10^6$),分别表示点 $A$ 的初始位置和期望的绝对差。
输出格式
对于每个测试用例,输出使得存在满足条件的点 $B$ 所需的最小步数。
说明/提示
在第一个测试用例(如上图),如果我们将 $B$ 的坐标设为 $2$,则绝对差为 $|(2 - 0) - (4 - 2)| = 0$,因此无需移动 $A$,答案为 $0$。
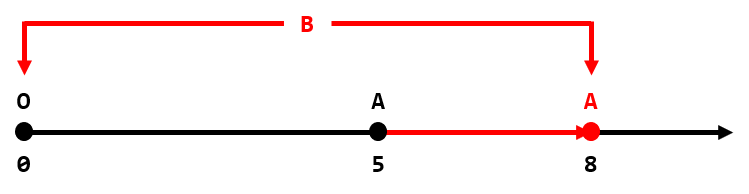
在第二个测试用例中,我们可以将 $A$ 的坐标增加 $3$,并将 $B$ 的坐标设为 $0$ 或 $8$。此时绝对差为 $|8 - 0| = 8$,所以答案为 $3$。
由 ChatGPT 4.1 翻译