Maximum Distributed Tree

# 题目描述 给定一棵 $n$ 个节点，$n-1$ 条边的树。你可以在每一条树上的边标上边权，使得： 1. 每个边权都为 **正整数**； 2. 这 $n-1$ 个边权的 **乘积** 等于 $k$； 3. 边权为 $1$ 的边的数量最少。 定义 $f(u,v)$ 表示节点 $u$ 到节点 $v$ 的简单路径经过的边权总和。你的任务是让 $\sum\limits_{i=1}^{n-1}\sum\limits_{j=i+1}^{n} f(i,j)$ 最大。 最终答案可能很大，对 $10^9+7$ 取模即可。 $k$ 有可能很大，输入数据中包含了 $m$ 个质数 $p_i$，那么 $k$ 为这些质数的乘积。 # 输入格式 第一行，一个整数 $t$ $(1\leq t\leq 100)$，表示多组测试数据个数。对于每一个测试数据： 第一行，一个整数 $n$ $(2\leq n\leq 10^5)$，表示树上节点数； 第 $2$ 至 $n$ 行，每行两个整数 $u_i$ 和 $v_i$ $(1\leq u_i,v_i \leq n,u_i\neq v_i)$，描述了一条无向边； 第 $n+1$ 行，一个整数 $m$ $(1\leq m\leq 6\times 10^4)$，表示 $k$ 分解成质因子的个数； 第 $n+2$ 行，$m$ 个 **质数** $p_i$ $(2\leq p_i< 6\times 10^4)$，有 $k=\prod\limits_{i=1}^m p_i$。 数据保证所有的 $n$ 总和不超过 $10^5$，所有的 $m$ 总和不超过 $6\times 10^4$。数据给出的边保证能够形成一棵树。 # 输出格式 一行，一个整数，表示最大的答案对 $10^9+7$ 取模后的值。

You are given a tree that consists of $ n $ nodes. You should label each of its $ n-1 $ edges with an integer in such way that satisfies the following conditions: - each integer must be greater than $ 0 $ ; - the product of all $ n-1 $ numbers should be equal to $ k $ ; - the number of $ 1 $ -s among all $ n-1 $ integers must be minimum possible. Let's define $ f(u,v) $ as the sum of the numbers on the simple path from node $ u $ to node $ v $ . Also, let $ \sum\limits_{i=1}^{n-1} \sum\limits_{j=i+1}^n f(i,j) $ be a distribution index of the tree. Find the maximum possible distribution index you can get. Since answer can be too large, print it modulo $ 10^9 + 7 $ . In this problem, since the number $ k $ can be large, the result of the prime factorization of $ k $ is given instead.

The first line contains one integer $ t $ ( $ 1 \le t \le 100 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ) — the number of nodes in the tree. Each of the next $ n-1 $ lines describes an edge: the $ i $ -th line contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ; $ u_i \ne v_i $ ) — indices of vertices connected by the $ i $ -th edge. Next line contains a single integer $ m $ ( $ 1 \le m \le 6 \cdot 10^4 $ ) — the number of prime factors of $ k $ . Next line contains $ m $ prime numbers $ p_1, p_2, \ldots, p_m $ ( $ 2 \le p_i < 6 \cdot 10^4 $ ) such that $ k = p_1 \cdot p_2 \cdot \ldots \cdot p_m $ . It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 10^5 $ , the sum of $ m $ over all test cases doesn't exceed $ 6 \cdot 10^4 $ , and the given edges for each test cases form a tree.

Print the maximum distribution index you can get. Since answer can be too large, print it modulo $ 10^9+7 $ .

3
4
1 2
2 3
3 4
2
2 2
4
3 4
1 3
3 2
2
3 2
7
6 1
2 3
4 6
7 3
5 1
3 6
4
7 5 13 3

17
18
286

In the first test case, one of the optimal ways is on the following image:  In this case, $ f(1,2)=1 $ , $ f(1,3)=3 $ , $ f(1,4)=5 $ , $ f(2,3)=2 $ , $ f(2,4)=4 $ , $ f(3,4)=2 $ , so the sum of these $ 6 $ numbers is $ 17 $ . In the second test case, one of the optimal ways is on the following image: 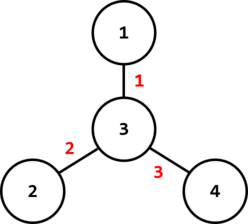 In this case, $ f(1,2)=3 $ , $ f(1,3)=1 $ , $ f(1,4)=4 $ , $ f(2,3)=2 $ , $ f(2,4)=5 $ , $ f(3,4)=3 $ , so the sum of these $ 6 $ numbers is $ 18 $ .