CF1408E Avoid Rainbow Cycles

You are given $ m $ sets of integers $ A_1, A_2, \ldots, A_m $ ; elements of these sets are integers between $ 1 $ and $ n $ , inclusive. There are two arrays of positive integers $ a_1, a_2, \ldots, a_m $ and $ b_1, b_2, \ldots, b_n $ . In one operation you can delete an element $ j $ from the set $ A_i $ and pay $ a_i + b_j $ coins for that. You can make several (maybe none) operations (some sets can become empty). After that, you will make an edge-colored undirected graph consisting of $ n $ vertices. For each set $ A_i $ you will add an edge $ (x, y) $ with color $ i $ for all $ x, y \in A_i $ and $ x < y $ . Some pairs of vertices can be connected with more than one edge, but such edges have different colors. You call a cycle $ i_1 \to e_1 \to i_2 \to e_2 \to \ldots \to i_k \to e_k \to i_1 $ ( $ e_j $ is some edge connecting vertices $ i_j $ and $ i_{j+1} $ in this graph) rainbow if all edges on it have different colors. Find the minimum number of coins you should pay to get a graph without rainbow cycles.

The first line contains two integers $ m $ and $ n $ ( $ 1 \leq m, n \leq 10^5 $ ), the number of sets and the number of vertices in the graph. The second line contains $ m $ integers $ a_1, a_2, \ldots, a_m $ ( $ 1 \leq a_i \leq 10^9 $ ). The third line contains $ n $ integers $ b_1, b_2, \ldots, b_n $ ( $ 1 \leq b_i \leq 10^9 $ ). In the each of the next of $ m $ lines there are descriptions of sets. In the $ i $ -th line the first integer $ s_i $ ( $ 1 \leq s_i \leq n $ ) is equal to the size of $ A_i $ . Then $ s_i $ integers follow: the elements of the set $ A_i $ . These integers are from $ 1 $ to $ n $ and distinct. It is guaranteed that the sum of $ s_i $ for all $ 1 \leq i \leq m $ does not exceed $ 2 \cdot 10^5 $ .

Print one integer: the minimum number of coins you should pay for operations to avoid rainbow cycles in the obtained graph.

In the first test, you can make such operations: - Delete element $ 1 $ from set $ 1 $ . You should pay $ a_1 + b_1 = 5 $ coins for that. - Delete element $ 1 $ from set $ 2 $ . You should pay $ a_2 + b_1 = 6 $ coins for that. You pay $ 11 $ coins in total. After these operations, the first and the second sets will be equal to $ \{2\} $ and the third set will be equal to $ \{1, 2\} $ . So, the graph will consist of one edge $ (1, 2) $ of color $ 3 $ . In the second test, you can make such operations: - Delete element $ 1 $ from set $ 1 $ . You should pay $ a_1 + b_1 = 11 $ coins for that. - Delete element $ 4 $ from set $ 2 $ . You should pay $ a_2 + b_4 = 13 $ coins for that. - Delete element $ 7 $ from set $ 3 $ . You should pay $ a_3 + b_7 = 13 $ coins for that. - Delete element $ 4 $ from set $ 4 $ . You should pay $ a_4 + b_4 = 16 $ coins for that. - Delete element $ 7 $ from set $ 6 $ . You should pay $ a_6 + b_7 = 13 $ coins for that. You pay $ 66 $ coins in total. After these operations, the sets will be: - $ \{2, 3\} $ ; - $ \{1\} $ ; - $ \{1, 3\} $ ; - $ \{3\} $ ; - $ \{3, 4, 5, 6, 7\} $ ; - $ \{5\} $ ; - $ \{8\} $ . 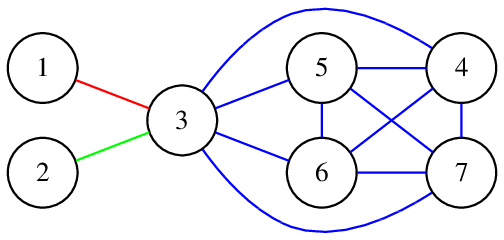We will get the graph:  There are no rainbow cycles in it.