CF1408E Avoid Rainbow Cycles

给定 $m$ 个整数集合 $A_1, A_2, \ldots, A_m$，这些集合的元素都是 $1$ 到 $n$ 之间的整数（包含 $1$ 和 $n$）。 有两个正整数数组 $a_1, a_2, \ldots, a_m$ 和 $b_1, b_2, \ldots, b_n$。 每次操作，你可以从集合 $A_i$ 中删除一个元素 $j$，并为此支付 $a_i + b_j$ 个金币。 你可以进行若干次（也可以不进行）这样的操作（有些集合可能会变成空集）。 之后，你将用这些集合构建一个带有边颜色的无向图，该图有 $n$ 个顶点。对于每个集合 $A_i$，对于所有 $x, y \in A_i$ 且 $x < y$，你都要添加一条颜色为 $i$ 的边 $(x, y)$。某些顶点对之间可能会有多条边，但这些边的颜色各不相同。 你称一个环 $i_1 \to e_1 \to i_2 \to e_2 \to \ldots \to i_k \to e_k \to i_1$（$e_j$ 是连接顶点 $i_j$ 和 $i_{j+1}$ 的某条边）为“彩虹环”，如果该环上的所有边颜色都不相同。 请你求出，为了使最终得到的图中没有彩虹环，你最少需要支付多少金币。

第一行包含两个整数 $m$ 和 $n$（$1 \leq m, n \leq 10^5$），分别表示集合的数量和图中顶点的数量。 第二行包含 $m$ 个整数 $a_1, a_2, \ldots, a_m$（$1 \leq a_i \leq 10^9$）。 第三行包含 $n$ 个整数 $b_1, b_2, \ldots, b_n$（$1 \leq b_i \leq 10^9$）。 接下来的 $m$ 行，每行描述一个集合。在第 $i$ 行，首先是一个整数 $s_i$（$1 \leq s_i \leq n$），表示 $A_i$ 的大小。接下来有 $s_i$ 个整数，表示 $A_i$ 的元素。这些整数在 $1$ 到 $n$ 之间且互不相同。 保证所有 $s_i$ 之和不超过 $2 \cdot 10^5$。

输出一个整数，表示为了避免彩虹环，你最少需要支付的金币数。

在第一个测试样例中，你可以进行如下操作： - 从第 $1$ 个集合中删除元素 $1$，需支付 $a_1 + b_1 = 5$ 个金币。 - 从第 $2$ 个集合中删除元素 $1$，需支付 $a_2 + b_1 = 6$ 个金币。 你总共支付了 $11$ 个金币。操作后，第 $1$、$2$ 个集合分别变为 $\{2\}$，第 $3$ 个集合为 $\{1, 2\}$。 这样，图中只剩下一条颜色为 $3$ 的边 $(1, 2)$。 在第二个测试样例中，你可以进行如下操作： - 从第 $1$ 个集合中删除元素 $1$，需支付 $a_1 + b_1 = 11$ 个金币。 - 从第 $2$ 个集合中删除元素 $4$，需支付 $a_2 + b_4 = 13$ 个金币。 - 从第 $3$ 个集合中删除元素 $7$，需支付 $a_3 + b_7 = 13$ 个金币。 - 从第 $4$ 个集合中删除元素 $4$，需支付 $a_4 + b_4 = 16$ 个金币。 - 从第 $6$ 个集合中删除元素 $7$，需支付 $a_6 + b_7 = 13$ 个金币。 你总共支付了 $66$ 个金币。 操作后，各集合变为： - $\{2, 3\}$； - $\{1\}$； - $\{1, 3\}$； - $\{3\}$； - $\{3, 4, 5, 6, 7\}$； - $\{5\}$； - $\{8\}$。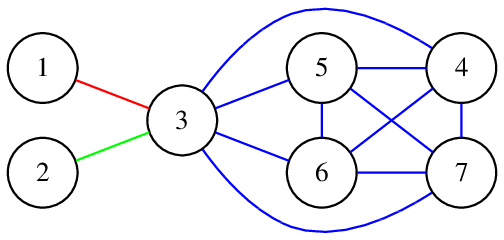 最终得到的图如下：  此时图中没有彩虹环。 由 ChatGPT 4.1 翻译