CF1409E Two Platforms

在平面上有 $n$ 个点，第 $i$ 个点的坐标为 $(x_i, y_i)$。你有两块长度为 $k$ 的水平平台。每个平台可以放在平面上的任意位置，但必须水平放置（即 $y$ 坐标相同），且左右边界的 $x$ 坐标均为整数。如果平台的左边界为 $(x, y)$，则右边界为 $(x + k, y)$，平台包含左右边界之间（包括边界）的所有点。 注意，两块平台可以有公共点（重叠），且不要求放在同一条 $y$ 轴上。 当你将两块平台放在平面上后，所有点会开始下落，即 $y$ 坐标不断减小。如果某个点在下落过程中碰到某个平台，则该点会停止下落并被“拯救”。那些永远不会碰到任何平台的点会丢失。 你的任务是，合理放置两块平台，使得被拯救的点数最多。 你需要回答 $t$ 组独立的测试用例。 为了更好地理解题意，请阅读下方的提示部分，查看第一个测试用例的示意图。

输入的第一行包含一个整数 $t$（$1 \le t \le 2 \cdot 10^4$），表示测试用例的数量。接下来是 $t$ 组测试用例。 每组测试用例的第一行包含两个整数 $n$ 和 $k$（$1 \le n \le 2 \cdot 10^5$；$1 \le k \le 10^9$），分别表示点的数量和每个平台的长度。第二行包含 $n$ 个整数 $x_1, x_2, \dots, x_n$（$1 \le x_i \le 10^9$），表示每个点的 $x$ 坐标。第三行包含 $n$ 个整数 $y_1, y_2, \dots, y_n$（$1 \le y_i \le 10^9$），表示每个点的 $y$ 坐标。所有点都互不相同（不存在 $1 \le i < j \le n$ 使得 $x_i = x_j$ 且 $y_i = y_j$）。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$（$\sum n \le 2 \cdot 10^5$）。

对于每组测试用例，输出一个整数，表示在最优放置平台的情况下，最多可以拯救多少个点。

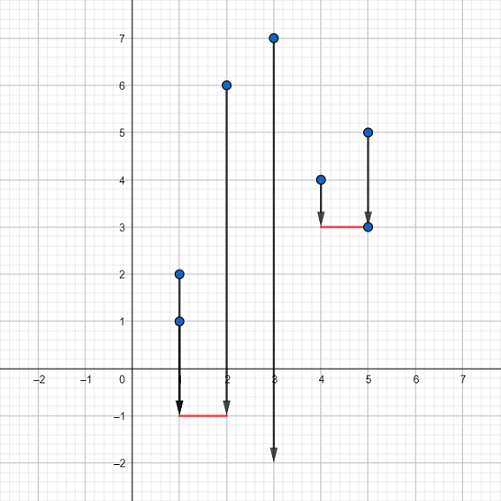
下图对应样例第一个测试用例：  蓝色点表示给定的点，红色线段表示平台。其中一种可行的放置方式是将第一块平台放在点 $(1, -1)$ 和 $(2, -1)$ 之间，第二块平台放在点 $(4, 3)$ 和 $(5, 3)$ 之间。箭头表示点的下落轨迹。可以看到，只有点 $(3, 7)$ 无法被拯救，会一直下落而丢失。可以证明这是最优方案。另外，点 $(5, 3)$ 已经在平台上，因此不会下落。 由 ChatGPT 4.1 翻译