CF1413C Perform Easily

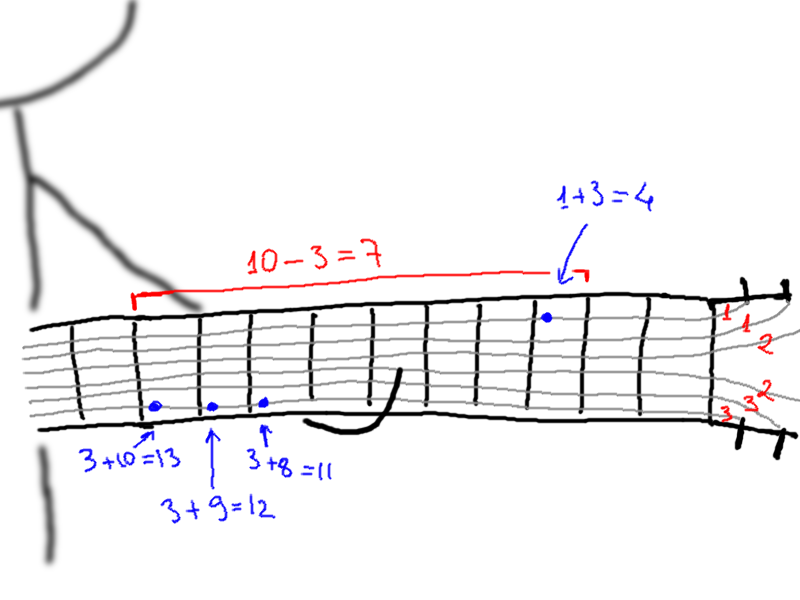
在与鹿丸战斗后，多由也觉得她的长笛太容易被预测，于是换成了一把吉他。这把吉他有 $6$ 根弦，并且有无限多品位，品位编号从 $1$ 开始。在第 $i$ 根弦按下第 $j$ 品时，会弹出音符 $a_{i} + j$。 多由也想要演奏一个包含 $n$ 个音符的旋律。每个音符可以用不同的弦和品位组合来弹奏。演奏的“容易度”取决于所用品位编号的最大值与最小值之差。这个差值越小，演奏就越容易。请你求出这个最小可能的差值。 例如，如果 $a = [1, 1, 2, 2, 3, 3]$，而音符序列为 $4, 11, 11, 12, 12, 13, 13$（对应第二个样例），我们可以将第一个音符弹在第一根弦，其余音符都弹在第六根弦上。此时最大品位为 $10$，最小品位为 $3$，答案就是 $10 - 3 = 7$，如图所示。 

第一行包含 $6$ 个用空格分隔的整数 $a_{1}, a_{2}, \ldots, a_{6}$（$1 \leq a_{i} \leq 10^{9}$），表示多由也吉他的每根弦。 第二行包含一个整数 $n$（$1 \leq n \leq 100\,000$），表示旋律中的音符数量。 第三行包含 $n$ 个用空格分隔的整数 $b_{1}, b_{2}, \ldots, b_{n}$（$1 \leq b_{i} \leq 10^{9}$），表示需要弹奏的音符。保证对于所有 $1\leq i\leq n$ 和 $1\leq j\leq 6$，都有 $b_i > a_j$，也就是说每个音符都可以在任意一根弦上弹奏。

输出所用品位编号最大值与最小值的最小可能差值。

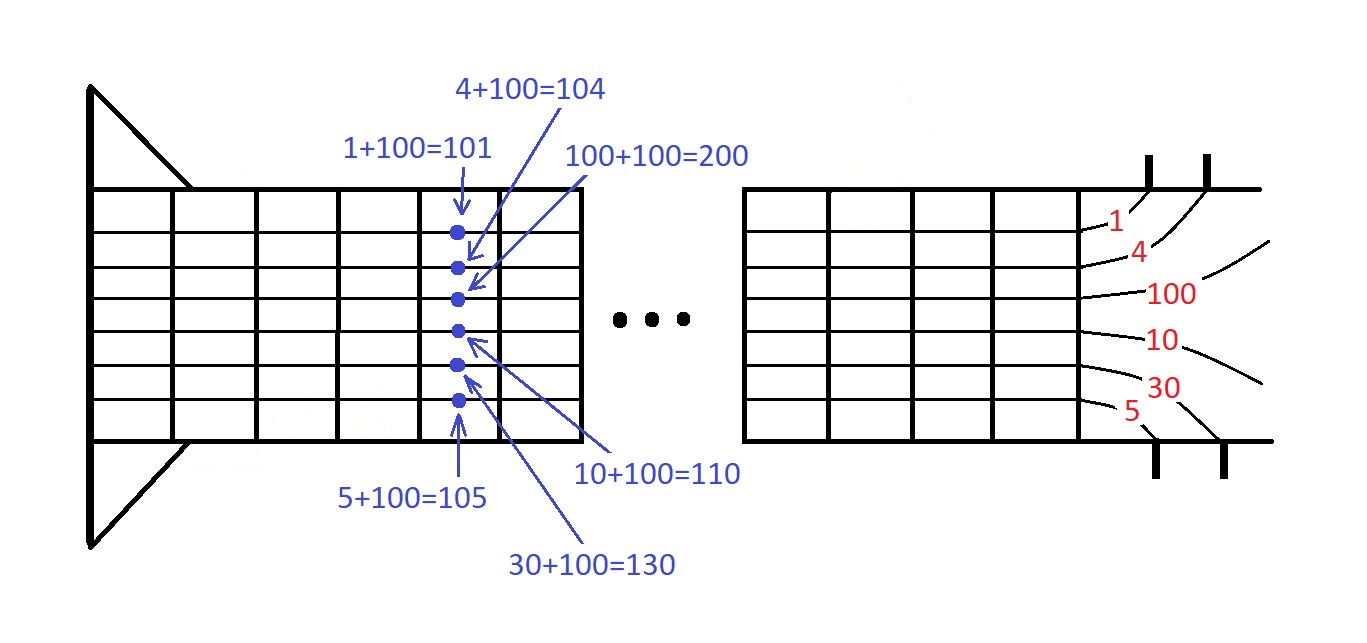
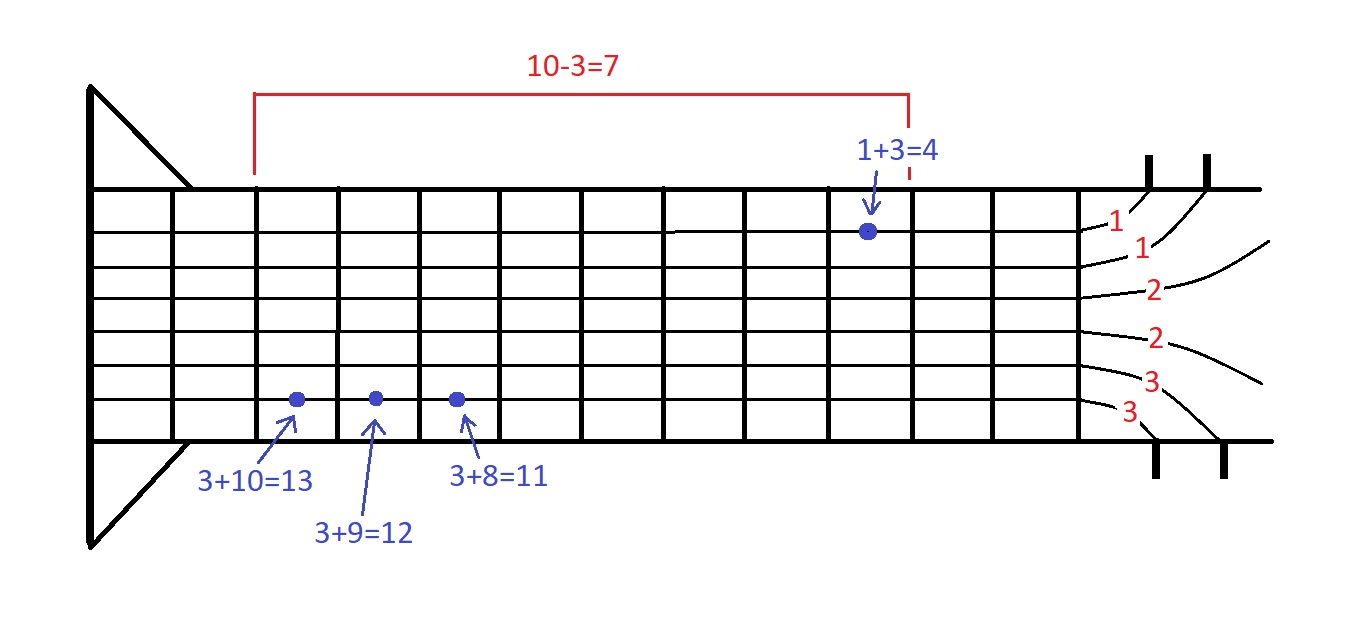
在第一个样例中，最优方案是将第一个音符弹在第一根弦，第二个音符弹在第二根弦，第三个音符弹在第六根弦，第四个音符弹在第四根弦，第五个音符弹在第五根弦，第六个音符弹在第三根弦。这样每次都用第 $100$ 品，差值为 $100 - 100 = 0$。  在第二个样例中，最优方案是比如将第二个音符弹在第一根弦，其余音符都弹在第六根弦。此时最大品位为 $10$，最小品位为 $3$，答案为 $10 - 3 = 7$。  由 ChatGPT 4.1 翻译