CF1421D Hexagons

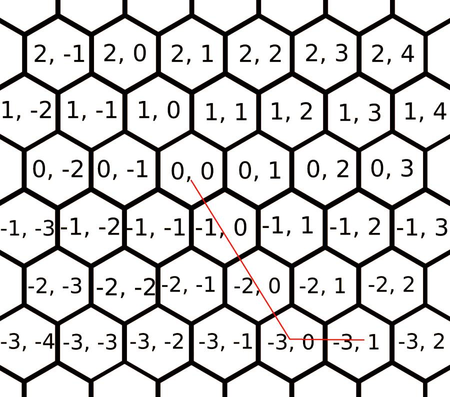
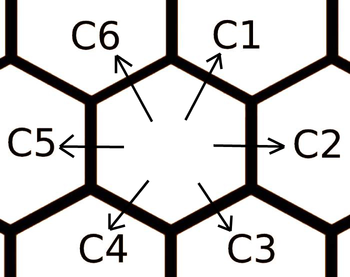
Lindsey Buckingham told Stevie Nicks ["Go your own way"](https://www.youtube.com/watch?v=6ul-cZyuYq4). Nicks is now sad and wants to go away as quickly as possible, but she lives in a 2D hexagonal world. Consider a hexagonal tiling of the plane as on the picture below. Nicks wishes to go from the cell marked $ (0, 0) $ to a certain cell given by the coordinates. She may go from a hexagon to any of its six neighbors you want, but there is a cost associated with each of them. The costs depend only on the direction in which you travel. Going from $ (0, 0) $ to $ (1, 1) $ will take the exact same cost as going from $ (-2, -1) $ to $ (-1, 0) $ . The costs are given in the input in the order $ c_1 $ , $ c_2 $ , $ c_3 $ , $ c_4 $ , $ c_5 $ , $ c_6 $ as in the picture below. Print the smallest cost of a path from the origin which has coordinates $ (0, 0) $ to the given cell.

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^{4} $ ). Description of the test cases follows. The first line of each test case contains two integers $ x $ and $ y $ ( $ -10^{9} \le x, y \le 10^{9} $ ) representing the coordinates of the target hexagon. The second line of each test case contains six integers $ c_1 $ , $ c_2 $ , $ c_3 $ , $ c_4 $ , $ c_5 $ , $ c_6 $ ( $ 1 \le c_1, c_2, c_3, c_4, c_5, c_6 \le 10^{9} $ ) representing the six costs of the making one step in a particular direction (refer to the picture above to see which edge is for each value).

For each testcase output the smallest cost of a path from the origin to the given cell.

The picture below shows the solution for the first sample. The cost $ 18 $ is reached by taking $ c_3 $ 3 times and $ c_2 $ once, amounting to $ 5+5+5+3=18 $ .