CF1421D Hexagons

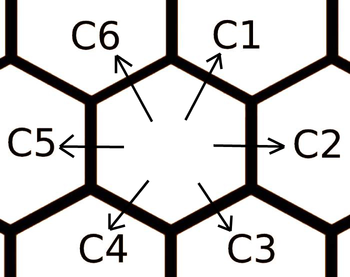
Lindsey Buckingham 对 Stevie Nicks 说了 ["Go your own way"](https://www.youtube.com/watch?v=6ul-cZyuYq4)。Nicks 现在很伤心，想尽快离开，但她生活在一个二维六边形世界中。 请考虑如下图所示的平面六边形镶嵌。  Nicks 希望从标记为 $(0, 0)$ 的单元格出发，前往给定坐标的某个单元格。她可以从一个六边形移动到任意一个相邻的六边形，但每个方向都有一个对应的花费。花费仅取决于你前进的方向。例如，从 $(0, 0)$ 到 $(1, 1)$ 的花费与从 $(-2, -1)$ 到 $(-1, 0)$ 的花费完全相同。输入中按照下图所示的顺序给出了 $c_1, c_2, c_3, c_4, c_5, c_6$ 六个方向的花费。  请输出从原点 $(0, 0)$ 到给定单元格的最小路径花费。

每组测试数据包含多个测试用例。第一行包含测试用例数量 $t$（$1 \le t \le 10^{4}$）。接下来是每组测试用例的描述。 每个测试用例的第一行包含两个整数 $x$ 和 $y$（$-10^{9} \le x, y \le 10^{9}$），表示目标六边形的坐标。 每个测试用例的第二行包含六个整数 $c_1, c_2, c_3, c_4, c_5, c_6$（$1 \le c_1, c_2, c_3, c_4, c_5, c_6 \le 10^{9}$），分别表示按上图顺序的六个方向每步的花费。

对于每个测试用例，输出从原点到目标单元格的最小路径花费。

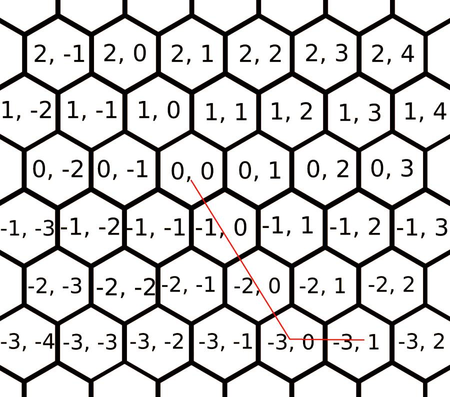
下图展示了第一个样例的解法。总花费 $18$ 是通过走 $c_3$ 三次和 $c_2$ 一次得到的，即 $5+5+5+3=18$。  由 ChatGPT 4.1 翻译