CF1423D Does anyone else hate the wind?

Mark 和他的船员正在穿越 Aeolus 之海（在希腊神话中，Aeolus 是风之守护者）。他们有一张地图，表示为 $N \times M$ 的矩阵，包含陆地和海洋格子，他们想要到达港口（港口被视为海洋格子）。由于那里风力强劲且多变，他们在海上只有 $K$ 天的食物（这是他们能携带的最大量）。Mark 的船员 John 能预测未来 $W$ 天的风向，这足够他们到达港口或耗尽食物。Mark 每天可以将船向四个方向（北、东、南、西）移动一格，也可以选择停留在原地。风可以向四个方向（北、东、南、西）吹，也可以当天无风。Aeolus 之海的风力非常强大，会将船整体吹动一格，方向由当天风向决定。船的最终移动是当天船员操作和风力共同作用的结果。Mark 必须小心，确保船只始终停留在海洋格子上，并且从起点出发到达的路径始终是 4 连通的海洋路径。4 连通路径指的是只能通过有公共边的格子相连。 例如，下图中，船无法到达港口，因为不存在通过海洋的 4 连通路径。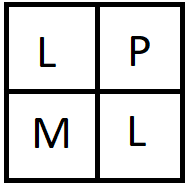  在下图中，船可以到达港口，红色箭头表示通过海洋的 4 连通路径。此外，如果出现以下情况之一，船可以在一步内到达港口：风向东吹且 Mark 向北移动，或风向北吹且 Mark 向东移动。在这两种情况下，船都能在一步内到达港口。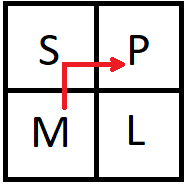  Mark 还必须确保船只不驶出地图，因为他不知道外面是什么。幸运的是，Mark 和他的船员在海上有 $T$ 个鱼铺可以补充食物，但每个鱼铺只在某一天营业。这意味着 Mark 和他的船员必须在鱼铺营业的那一天正好到达该位置，才能补充食物至最大量。请帮助 Mark 计算他和船员到达港口所需的最少天数，或者如果无法在现有食物供应下到达港口，则输出 $-1$。

第一行包含两个整数 $N$ 和 $M$（$1 \leq N, M \leq 200$），表示地图的行数和列数。 第二行包含三个整数，$K$（$0 \leq K \leq 200$），表示可用食物天数，$T$（$0 \leq T \leq 20$），表示可补给食物的格子数，$W$（$0 \leq W \leq 10^6$），表示有风向信息的天数。 接下来是 $N \times M$ 的字符矩阵，包含 'L'、'S'、'P' 或 'M'。'L' 表示陆地，'S' 表示海洋，'P' 表示港口，'M' 表示船的起始位置。 下一行包含 $W$ 个字符，表示每天的风向信息。可能的输入为 'N'（北）、'S'（南）、'E'（东）、'W'（西）、'C'（无风）。如果 Mark 的船员能到达港口，保证不需要超过 $W$ 天。 最后有 $T$ 行，每行包含三个整数，$Y_i$ 和 $X_i$（$0 \leq Y_i < N, 0 \leq X_i < M$），表示补给点的坐标（$Y$ 为行号，$X$ 为列号），以及 $F_i$（$0 \leq F_i \leq 10^6$），表示该补给点营业的天数（从第 0 天开始计）。

输出一个整数，表示到达港口所需的最少天数。如果无法到达港口，则输出 $-1$。

由 ChatGPT 4.1 翻译