CF1425D Danger of Mad Snakes

忍者 Chanek 先生有一天接到一个任务，要处理正在袭击某地的疯狂蛇群。现在，Chanek 先生已经到达了山丘，而目标地点就在这些山丘正下方。任务区域可以划分为 $1000 \times 1000$ 的方格。有 $N$ 条疯狂蛇，第 $i$ 条疯狂蛇位于方格 $(X_i, Y_i)$，其危险等级为 $B_i$。 Chanek 先生打算使用他从第七代火影那里学到的影分身术和螺旋丸来完成这个任务。他的攻击策略如下： 1. Chanek 先生将制造 $M$ 个分身。 2. 每个分身会选择一条疯狂蛇作为攻击目标。每个分身必须选择不同的疯狂蛇进行攻击。 3. 所有分身会同时从山丘跳下，用半径为 $R$ 的螺旋丸攻击各自选定的目标。如果位于方格 $(X, Y)$ 的疯狂蛇被直接攻击，则它和所有位于方格 $(X', Y')$ 满足 $ \max(|X' - X|, |Y' - Y|) \le R $ 的疯狂蛇都会被消灭。 4. 本体 Chanek 先生会计算这次攻击的得分。得分定义为所有被消灭的疯狂蛇的危险等级之和的平方。 现在 Chanek 先生很好奇，所有可能的攻击策略的得分之和是多少？由于这个数字可能非常大，他只需要输出结果对 $10^9 + 7$ 取模后的值即可。

第一行包含三个整数 $N$、$M$、$R$，分别表示疯狂蛇的数量、分身的数量和螺旋丸的半径，满足 $1 \le M \le N \le 2 \cdot 10^3, 0 \le R < 10^3$。 接下来的 $N$ 行，每行包含三个整数 $X_i$、$Y_i$、$B_i$，分别表示第 $i$ 条疯狂蛇的位置和危险等级，满足 $1 \le X_i, Y_i \le 10^3, 1 \le B_i \le 10^6$。保证没有两条疯狂蛇占据同一个方格。

输出一行，表示所有可能攻击策略的得分之和。

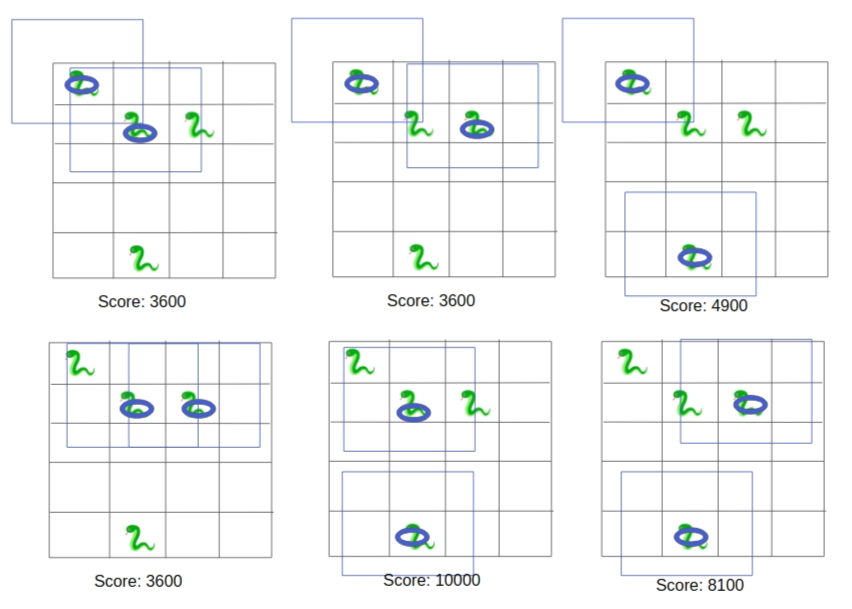
下图展示了所有六种可能的攻击策略。圆圈表示被选中的疯狂蛇，蓝色方块表示螺旋丸的攻击范围：  因此，所有攻击的总得分为：$3\,600 + 3\,600 + 4\,900 + 3\,600 + 10\,000 + 8\,100 = 33\,800$。 由 ChatGPT 4.1 翻译