CF1428G2 Lucky Numbers (Hard Version)

This is the hard version of the problem. The only difference is in the constraint on $ q $ . You can make hacks only if all versions of the problem are solved. Zookeeper has been teaching his $ q $ sheep how to write and how to add. The $ i $ -th sheep has to write exactly $ k $ non-negative integers with the sum $ n_i $ . Strangely, sheep have superstitions about digits and believe that the digits $ 3 $ , $ 6 $ , and $ 9 $ are lucky. To them, the fortune of a number depends on the decimal representation of the number; the fortune of a number is equal to the sum of fortunes of its digits, and the fortune of a digit depends on its value and position and can be described by the following table. For example, the number $ 319 $ has fortune $ F_{2} + 3F_{0} $ . 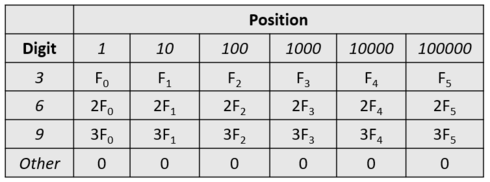Each sheep wants to maximize the sum of fortune among all its $ k $ written integers. Can you help them?

The first line contains a single integer $ k $ ( $ 1 \leq k \leq 999999 $ ): the number of numbers each sheep has to write. The next line contains six integers $ F_0 $ , $ F_1 $ , $ F_2 $ , $ F_3 $ , $ F_4 $ , $ F_5 $ ( $ 1 \leq F_i \leq 10^9 $ ): the fortune assigned to each digit. The next line contains a single integer $ q $ ( $ 1 \leq q \leq 100\,000 $ ): the number of sheep. Each of the next $ q $ lines contains a single integer $ n_i $ ( $ 1 \leq n_i \leq 999999 $ ): the sum of numbers that $ i $ -th sheep has to write.

Print $ q $ lines, where the $ i $ -th line contains the maximum sum of fortune of all numbers of the $ i $ -th sheep.

In the first test case, $ 57 = 9 + 9 + 39 $ . The three $ 9 $ 's contribute $ 1 \cdot 3 $ and $ 3 $ at the tens position contributes $ 2 \cdot 1 $ . Hence the sum of fortune is $ 11 $ . In the second test case, $ 63 = 35 + 19 + 9 $ . The sum of fortune is $ 8 $ .