CF1428H Rotary Laser Lock

为了防止这些顽皮的兔子在动物园里自由游荡，动物园管理员为兔子圈设置了一个特殊的锁。这种锁叫做旋转激光锁。 - 锁由编号为 $0$ 到 $n−1$ 的 $n$ 个同心环组成。最里面的环是环 $0$，最外面的环是环 $n−1$。 - 所有环平均分成 $n\times m$ 部分。这些环中的每一个都包含一个金属圆弧，正好覆盖了 $m$ 个相邻的部分。 - 在环的中心是一个核心。有 $n\times m$ 接收器围绕着整个锁，对准 $n\times m$ 个部分。 - 核心有 $n\times m$ 个激光器，从中心中的每个部分向外照射。激光可以被任何一个电弧阻挡。锁外面的显示屏显示有多少激光击中了外部接收器。 （见上图） 在上例中，有 $n=3$ 个环，每个环覆盖 $m=4$ 个截面。弧线的颜色为绿色（环 $0$ ）、紫色（环 $1$ ）和蓝色（环$2$ ），而激光束显示为红色。 有 $n\times m=12$ 段，$3$ 个激光器没有被任何弧光阻挡，因此在这种情况下显示器将显示 $3$。 Wabbit 试图打开锁释放兔子，但锁是完全不透明的，他看不见任何弧线在哪里。如果给出弧的相对位置，Wabbit 可以自己打开锁。 准确地说，Wabbit需要 $n-1$ 个整数 $p_1，p_2，\ldots，p_{n-1}$ 作为相对位置，满足对于任意的 $1\leqslant i< n$，有 $0 \leqslant p_i\leqslant n\times m$。 Wabbit 要顺时针旋转环 $0$ 恰好 $p_i$ 次，使环 $0$ 覆盖的部分与环 $i$ 覆盖的部分完全对齐。 在上面的例子中，相对位置 $p_1=1,p_2=7$。 他可以选择 $n$ 个环中的任意一个，并将其顺时针或逆时针旋转 $1$ 段。每次旋转后，您将在显示屏上看到数字。 因为 Wabbit 的爪子很小，他让你帮他找到他所有的位置。在 Wabbit 失去耐心之前，你可以让他旋转最多 $15000$ 次。

第一行包含两个整数 $n$ 和 $m$ $(2\leqslant n \leqslant 100,2\leqslant m \leqslant 20)$，表示环的数量和每个环覆盖的部分的数量。

要执行旋转，请在输出一行 ``? x d``，满足 $(0\leqslant x

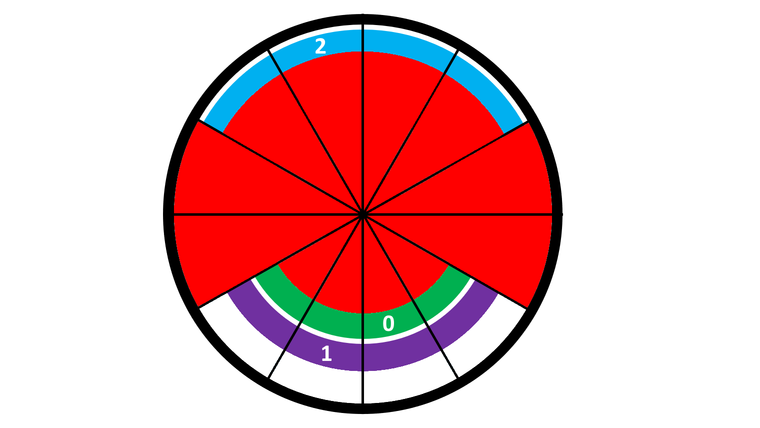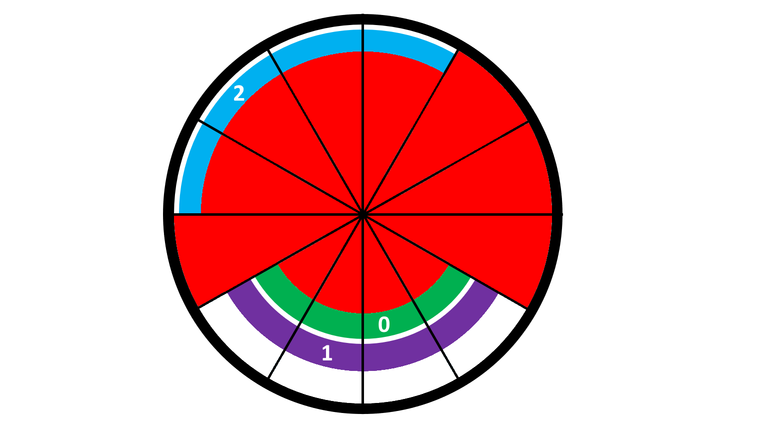For the first test, the configuration is the same as shown on the picture from the statement. 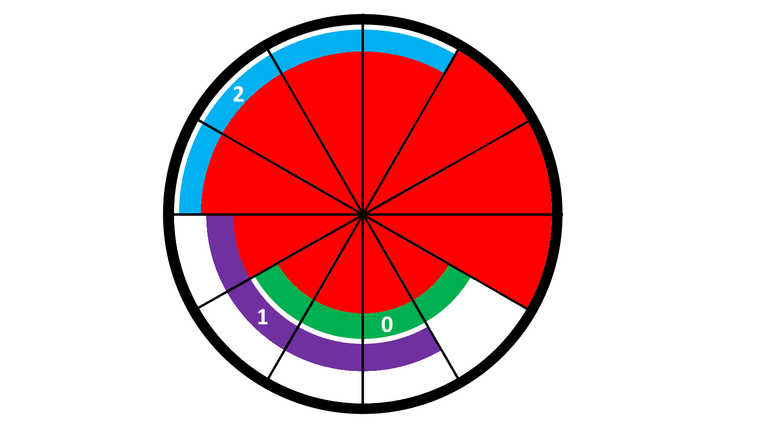After the first rotation (which is rotating ring $ 0 $ clockwise by $ 1 $ section), we obtain the following configuration: After the second rotation (which is rotating ring $ 2 $ counter-clockwise by $ 1 $ section), we obtain the following configuration: After the third rotation (which is rotating ring $ 1 $ clockwise by $ 1 $ section), we obtain the following configuration: If we rotate ring $ 0 $ clockwise once, we can see that the sections ring $ 0 $ covers will be the same as the sections that ring $ 1 $ covers, hence $ p_1=1 $ . If we rotate ring $ 0 $ clockwise five times, the sections ring $ 0 $ covers will be the same as the sections that ring $ 2 $ covers, hence $ p_2=5 $ . Note that if we will make a different set of rotations, we can end up with different values of $ p_1 $ and $ p_2 $ at the end.