CF1433G Reducing Delivery Cost

你是 Berlyatov 的市长。该城市有 $n$ 个区和 $m$ 条双向道路，第 $i$ 条道路连接区 $x_i$ 和区 $y_i$，该道路的通行费用为 $w_i$。任意两个区之间都存在一条路径，因此整个城市是连通的。 Berlyatov 有 $k$ 条快递路线。第 $i$ 条路线从区 $a_i$ 送到区 $b_i$。每条路线有一名快递员，快递员总是选择从 $a_i$ 到 $b_i$ 的最便宜（总费用最小）的路径来送货。 路线可以从某个区到自身，不同快递员的路线可能重合（需要分别计算）。 你可以将至多一条道路的费用变为 $0$（即你可以选择至多一条道路，将其费用改为 $0$）。 设 $d(x, y)$ 表示从区 $x$ 到区 $y$ 的最小通行费用。 你的任务是，若你可以最优地选择一条道路并将其费用变为 $0$，求所有快递路线的总费用最小值，即最小化 $ \sum\limits_{i = 1}^{k} d(a_i, b_i) $。

输入的第一行包含三个整数 $n$、$m$ 和 $k$（$2 \le n \le 1000$；$n - 1 \le m \le \min(1000, \frac{n(n-1)}{2})$；$1 \le k \le 1000$），分别表示区的数量、道路的数量和快递路线的数量。 接下来的 $m$ 行描述道路。第 $i$ 行包含三个整数 $x_i$、$y_i$ 和 $w_i$（$1 \le x_i, y_i \le n$；$x_i \ne y_i$；$1 \le w_i \le 1000$），表示第 $i$ 条道路连接区 $x_i$ 和区 $y_i$，通行费用为 $w_i$。保证任意两个区之间都存在路径，整个城市连通。保证任意一对区之间至多有一条道路。 接下来的 $k$ 行描述快递路线。第 $i$ 行包含两个整数 $a_i$ 和 $b_i$（$1 \le a_i, b_i \le n$），表示第 $i$ 条快递路线从区 $a_i$ 到区 $b_i$。路线可以从某区到自身，不同快递员的路线可能重合（需要分别计算）。

输出一个整数，表示在最优地选择一条道路并将其费用变为 $0$ 后，所有快递路线的总费用的最小值（即 $ \sum\limits_{i=1}^{k} d(a_i, b_i) $ 的最小值，其中 $d(x, y)$ 表示从区 $x$ 到区 $y$ 的最小通行费用）。

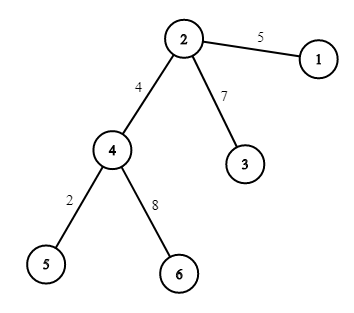
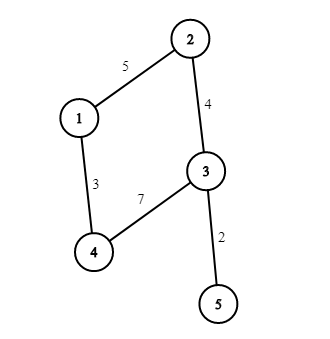
第一个样例对应的图如下：  在该图中，你可以选择道路 $(2, 4)$ 或 $(4, 6)$，两种选择都能使总费用变为 $22$。 第二个样例对应的图如下：  在该图中，你可以选择道路 $(3, 4)$，这样总费用为 $13$。 由 ChatGPT 4.1 翻译