CF1437D Minimal Height Tree
题目描述
Monocarp 有一棵包含 $n$ 个结点、以结点 $1$ 为根的树。他决定学习广度优先搜索(BFS),于是他从根节点开始对树进行 BFS。BFS 可以用如下伪代码描述:
```
a = [] # 记录被访问结点的顺序
q = Queue()
q.put(1) # 将根节点放入队列末尾
while not q.empty():
k = q.pop() # 取出队首结点
a.append(k) # 将 k 加入访问顺序序列末尾
for y in g[k]: # g[k] 表示结点 k 的所有子节点,按升序排列
q.put(y)
```
Monocarp 对 BFS 十分着迷,结果最后把树弄丢了。幸运的是,他还保留着 BFS 访问结点的顺序(即伪代码中的数组 $a$)。Monocarp 知道每个结点都被访问且仅被访问一次(因为每个结点仅被放入和取出队列一次)。此外,他还知道每个结点的所有子节点都是按升序访问的。
Monocarp 知道一般情况下有许多棵树会有相同的访问顺序 $a$,所以他并不指望还原出原来的树。Monocarp 满足于找到任意一棵高度最小的树。
树的高度定义为所有结点的最大深度,结点的深度是从根到该结点路径上的边数。例如,根节点 $1$ 的深度为 $0$,根节点的所有子节点深度为 $1$。
请你帮助 Monocarp,给定 BFS 访问顺序 $a$,找出任意一棵高度最小的树,并输出其最小可能高度。
输入格式
第一行包含一个整数 $t$($1 \le t \le 1000$),表示测试用例的数量。
每个测试用例的第一行包含一个整数 $n$($2 \le n \le 2 \cdot 10^5$),表示树的结点数。
每个测试用例的第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$($1 \le a_i \le n$;$a_i \neq a_j$;$a_1 = 1$),表示 BFS 访问结点的顺序。
保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。
输出格式
对于每个测试用例,输出一个整数,表示具有给定访问顺序 $a$ 的树的最小可能高度。
说明/提示
在第一个测试用例中,只有一棵树满足给定的访问顺序:
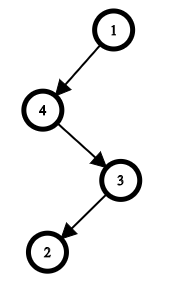
在第二个测试用例中,也只有一棵树满足给定的访问顺序:
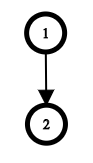
在第三个测试用例中,最优的树如下图所示:
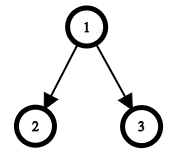
由 ChatGPT 4.1 翻译