CF1442F Differentiating Games

这是一个交互题。 Ginny 正在参加一场关于博弈论的考试。教授厌倦了一遍又一遍地听到相同的答案，于是他提出让 Ginny 玩一个游戏，代替传统的考试。 正如课程中所学，图上的组合游戏（combinatorial game）是指在一个有向图上，有多个起始位置，每个起始位置上各有一个棋子。两名玩家轮流操作，每次可以选择一个棋子，沿着图上的有向边移动一步。无法进行操作的玩家判负。如果双方都能无限进行下去而不输，则判为平局。 在考试中，教授画出了一个有向无环图，并选择了其中的一个顶点。Ginny 需要猜出教授选中的顶点。为此，Ginny 可以多次选择一个顶点多重集 $S$，并向教授提问：“如果我在图中每个 $S$ 中出现的顶点各放一个棋子，再在被选中的顶点上再放一个棋子，这个组合游戏的结果会如何？” 教授布置完任务后，离开了教室，让 Ginny 有时间准备。Ginny 觉得自己被耍了，因为她认为这个问题无法解决。因此，在教授离开期间，她想要在图上添加或删除一些边。虽然原始图是无环的，但添加边后可能会出现环。

本题的交互分为若干阶段。 在第一阶段，交互器会输入三个整数 $N$（$1 \le N \le 1000$）、$M$（$0 \le M \le 100\,000$）、$T$（$1 \le T \le 2000$）：分别表示初始图的顶点数、边数，以及 Ginny 需要猜测被选中顶点的次数。接下来的 $M$ 行，每行包含两个整数 $a_i$ $b_i$（$1 \le a_i, b_i \le N$），表示一条从 $a_i$ 到 $b_i$ 的有向边。保证图是有向无环图，且所有边互不相同。 你的程序应输出一个整数 $K$（$0 \le K \le 4242$），表示需要对图进行修改的边数。接下来的 $K$ 行，每行形如 "+ $a_i$ $b_i$" 或 "- $a_i$ $b_i$"，分别表示添加或删除一条从 $a_i$ 到 $b_i$ 的边。允许添加已存在的边。操作按顺序执行，因此可以删除刚刚添加的边。只能删除已存在的边。操作可能会导致图中出现环。 接下来的 $T$ 个阶段用于猜测被选中的顶点。在每个阶段中，程序最多可以进行 20 次查询，然后输出答案。每次查询一个多重集 $S$，应输出 "? $|S|~S_1~S_2~\dots~S_{|S|}$"。每个阶段所有多重集元素个数之和不得超过 20。交互器会回复以下之一： - "Win"：若在多重集 $S$ 和被选中顶点上各放一个棋子后，组合游戏的胜者是先手。 - "Lose"：若胜者是后手。 - "Draw"：若游戏以平局结束。 - "Slow"：若本阶段查询次数达到 21 次，或所有多重集元素个数之和超过 20。此时程序应终止，并会收到 Wrong Answer 判定。 一旦确定被选中的顶点，应输出 "! v"。如果猜对了，交互器会输出 "Correct"，程序应进入下一阶段或结束。如果猜错了，交互器会输出 "Wrong"，程序应终止并收到 Wrong Answer 判定。 交互器可以根据图的变化和你的操作更改被选中的顶点，但在任何时刻，至少存在一个顶点与所有已给出的交互器答案一致。 Hack 格式 Hack 有以下额外限制： - $T = 1$ - 你需要指定一个被交互器选中的顶点。 Hack 测试格式：输入第一行为三个整数 $N~M~1$。接下来的 $M$ 行为边的描述，格式同上。最后一行为一个整数 $v$，表示被选中的顶点编号。即使你猜对了顶点，但该顶点不是唯一与所有查询结果一致的顶点，Hack 也会判定成功。

见上文交互说明。

在样例测试中，空行表示等待对方输入。真实交互器不会输出空行，程序也不应输出空行。 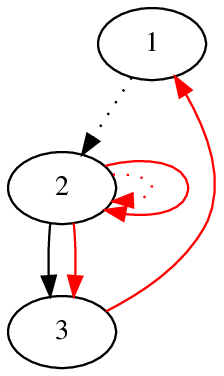 上图展示了样例测试。红色为新增边，虚线为被删除的边。三个猜测阶段分别展示了不同的解法。 - 如果只查询被选中的顶点，交互器会返回该顶点上游戏的结果。仅当被选中的顶点编号为 $1$ 时，先手才会输。 - 如果在被选中的顶点上再加一个顶点 $2$，那么若被选中的顶点是 $1$ 或 $2$，游戏应为平局。若被选中的顶点是 $3$，则先手获胜。 - 如果在顶点 $1$ 上放三个棋子，在顶点 $3$ 上放两个棋子，游戏仅当被选中顶点为 $2$ 时为平局。若被选中顶点为 $3$，先手获胜；若为 $1$，后手获胜。 在第一个测试中，交互器的行为与上述示例一致。但如果你在唯一确定答案前就尝试猜测，程序会收到 "Wrong Answer"，即使你输出的答案是正确的。因为交互器允许在保证与所有查询结果一致的情况下更改被选中的顶点。 由 ChatGPT 4.1 翻译