CF1444C Team-Building

新学年开始了，Berland 大学有 $n$ 名一年级新生。他们被分成了 $k$ 个学术小组，但有些小组可能是空的。在这些学生中，有 $m$ 对相互认识的同学，每一对认识的同学可能在同一个小组，也可能在不同的小组。 Alice 是一年级新生的辅导员，她想举办一个有趣的游戏，让大家都能互相认识。为此，她会选择两个不同的学术小组，然后将这两个小组的学生分成两队。游戏要求每一队内部不能有任何一对相互认识的同学。 Alice 想知道，有多少对小组可以被选出来，使得能够分成两队来进行游戏。被选中的两个小组的所有学生都必须参与游戏。 请注意，Alice 分队时，队伍成员不需要和原来的小组完全一致。此外，两队的人数可以不同（甚至可以为空）。

第一行包含三个整数 $n$、$m$ 和 $k$（$1 \le n \le 500\,000$；$0 \le m \le 500\,000$；$2 \le k \le 500\,000$），分别表示学生人数、认识的同学对数和小组数。 第二行包含 $n$ 个整数 $c_1, c_2, \dots, c_n$（$1 \le c_i \le k$），其中 $c_i$ 表示第 $i$ 个学生所在的小组编号。 接下来 $m$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \le a_i, b_i \le n$），表示学生 $a_i$ 和 $b_i$ 互相认识。保证 $a_i \neq b_i$，且每对无序的学生对只出现一次。

输出一个整数，表示可以选择多少对不同的小组，使得能够分成两队进行游戏。

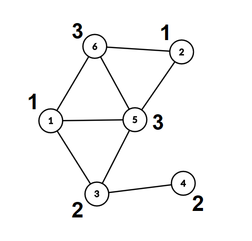
下图展示了第一个样例的认识关系图（每个学生旁边标注了其小组编号）。  在该测试中，可以选择以下小组对： - 选择第 1 组和第 2 组。例如，一队可以由学生 $1$ 和 $4$ 组成，另一队可以由学生 $2$ 和 $3$ 组成。 - 选择第 2 组和第 3 组。例如，一队可以由学生 $3$ 和 $6$ 组成，另一队可以由学生 $4$ 和 $5$ 组成。 - 不能选择第 1 组和第 3 组，因为无法将学生分成满足条件的两队。 在第二个样例中，可以选择任意一对小组。请注意，即使第三组没有学生，也可以和其他组一起被选中。 由 ChatGPT 4.1 翻译