CF1444D Rectangular Polyline
题目描述
在平面上画了一条闭合折线,这条折线只由垂直和水平的线段组成(与坐标轴平行)。这些线段在水平方向和垂直方向之间交替出现(即每条水平线段后面必有一条垂直线段,反之亦然)。这条折线没有严格的自交,也就是说,如果有两条线段有公共点,那么这个点一定是它们的端点(请参考提示部分的示例)。
不幸的是,这条折线已经被擦掉了,你只知道所有水平和垂直线段的长度。请你构造出任意一条满足描述的折线,或者判断这样的折线不存在。
输入格式
第一行包含一个整数 $t$($1 \leq t \leq 200$),表示测试用例的数量。
每个测试用例的第一行包含一个整数 $h$($1 \leq h \leq 1000$),表示水平线段的数量。接下来一行包含 $h$ 个整数 $l_1, l_2, \dots, l_h$($1 \leq l_i \leq 1000$),表示折线的水平线段的长度,顺序任意。
接下来一行包含一个整数 $v$($1 \leq v \leq 1000$),表示垂直线段的数量,下一行包含 $v$ 个整数 $p_1, p_2, \dots, p_v$($1 \leq p_i \leq 1000$),表示折线的垂直线段的长度,顺序任意。
测试用例之间用一个空行分隔,所有测试用例中 $h + v$ 的总和不超过 $1000$。
输出格式
对于每个测试用例,如果存在至少一条满足要求的折线,输出 Yes,否则输出 No。如果存在这样的折线,接下来 $n$ 行输出折线顶点的坐标,按照折线遍历的顺序输出:第 $i$ 行输出两个整数 $x_i$ 和 $y_i$,表示第 $i$ 个顶点的坐标。
注意,每条折线段必须是水平或垂直的,并且线段应当交替出现。坐标的绝对值不应超过 $10^9$。
说明/提示
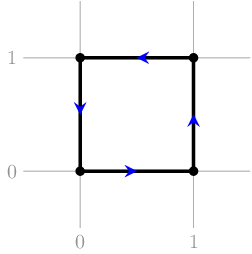
在第一个示例的第一个测试用例中,答案是 Yes——例如,下面的图展示了一个满足要求的正方形:
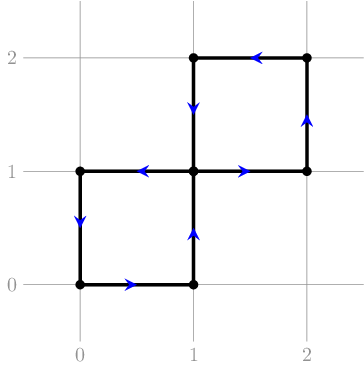
在第二个示例的第一个测试用例中,也存在满足要求的折线。注意,折线包含自交,但仅在端点处:
在第二个示例的第二个测试用例中,满足要求的折线可能如下所示:

注意,下面的折线不是合法的,因为它存在不在端点的自交:

由 ChatGPT 4.1 翻译