CF1446C Xor Tree

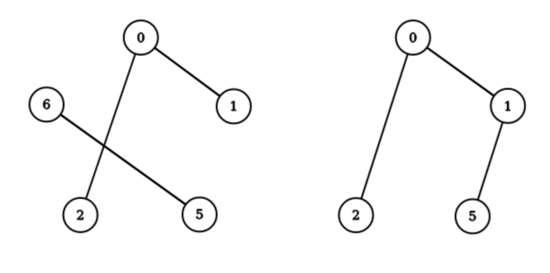
给定一个由互不相同的非负整数构成的序列 $(b_1, b_2, \dots, b_k)$，我们按照如下方式判断该序列是否为“好”序列： - 考虑一个有 $k$ 个节点的无向图，每个节点上分别写着 $b_1$ 到 $b_k$ 这 $k$ 个数。 - 对于每个 $i$（$1 \leq i \leq k$）：找到一个 $j$（$1 \leq j \leq k$，$j \neq i$），使得 $b_i \oplus b_j$ 在所有满足条件的 $j$ 中最小，其中 $\oplus$ 表示按位异或操作。然后，在编号为 $b_i$ 和 $b_j$ 的节点之间连一条无向边。 - 如果最终得到的图是一棵树（即连通且无环），则称该序列为“好”序列。 注意，对于某些 $b_i$ 和 $b_j$，可能会尝试两次在它们之间连边，但实际上只连一次。 下面给出一个例子（对应第一个测试用例的图片）。 序列 $(0, 1, 5, 2, 6)$ 不是“好”序列，因为无法从 $5$ 到达 $1$。 然而，序列 $(0, 1, 5, 2)$ 是“好”序列。  现在给定一个由互不相同的非负整数构成的序列 $(a_1, a_2, \dots, a_n)$，你可以删除其中的一些元素（也可以一个都不删），使得剩下的序列是“好”序列。请问，最少需要删除多少个元素，才能使剩下的序列是“好”序列？ 可以证明，对于任意序列，总可以删除一些元素，至少剩下 $2$ 个数，使得剩下的序列是“好”序列。

第一行包含一个整数 $n$（$2 \leq n \leq 200\,000$），表示序列的长度。 第二行包含 $n$ 个互不相同的非负整数 $a_1, a_2, \ldots, a_n$（$0 \leq a_i \leq 10^9$），表示序列中的元素。

输出一个整数，表示最少需要删除多少个元素，才能使剩下的序列是“好”序列。

注意，被删除的数字不会影响判断剩下的序列是否为“好”序列。 对于某些 $b_i$ 和 $b_j$，可能会尝试两次在它们之间连边，但实际上只连一次。 由 ChatGPT 4.1 翻译