CF144B Meeting

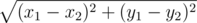
超级秘密军事小队的超级秘密会议在一个超级秘密的地方举行。该地方是一个无限平面，并引入了笛卡尔坐标系。会议桌被表示为一个矩形，其边平行于坐标轴，且顶点位于平面上的整数点。在属于桌子边界的每个整数点上都放有一把椅子，椅子上坐着一位将军。 平面上的某些点设置有取暖器，以防冬天将军们被冻着。每个取暖器具有一个数 $r_{i}$，表示该取暖器能加热的半径区域。也就是说，如果某位将军与某个取暖器之间的距离小于等于 $r_{i}$，则该将军会感到舒适温暖。这里距离按照欧几里得距离计算，即点 $(x_{1},y_{1})$ 和 $(x_{2},y_{2})$ 之间的距离为  每位位于取暖器加热范围之外的将军有可能生病。因此，你需要为他们准备毛毯。你的任务是计算需要带多少条毛毯去超级秘密地方。 已经感到温暖舒适的将军不需要盖毛毯。即使有多组取暖器加热到同一位置，将军也不会感到过热。取暖器可以放在平面的任意整数点上，甚至可以放在矩形内（桌子下方）或边界上（就在某位将军正下方）。即使如此，它们的加热半径不会发生变化。

第一行输入会议桌的两个对角点坐标 $x_{a}$、$y_{a}$、$x_{b}$、$y_{b}$（$x_{a} \ne x_{b},\, y_{a} \ne y_{b}$）。 第二行输入整数 $n$，表示取暖器数量（$1 \le n \le 10^{3}$）。 接下来的 $n$ 行，每行输入一个取暖器的坐标和半径，用“$x_{i}\ y_{i}\ r_{i}$”表示，数字以空格分隔。所有输入数据均为整数。所有坐标的绝对值不超过 $1000$，$1 \le r_{i} \le 1000$。同一位置可以放多个取暖器。

输出一个整数——你需要带的毛毯数量。

在第一个样例中，将军坐在以下几个点：$(2,2)$，$(2,3)$，$(2,4)$，$(2,5)$，$(3,2)$，$(3,5)$，$(4,2)$，$(4,3)$，$(4,4)$，$(4,5)$。其中有 4 位将军处于加热范围之外，分别为 $(2,5)$、$(3,5)$、$(4,4)$、$(4,5)$。 在第二个样例中，将军坐在以下几个点：$(5,2)$，$(5,3)$，$(6,2)$，$(6,3)$。这些将军全部都在取暖器的加热范围之内。 由 ChatGPT 5 翻译