CF144E Competition

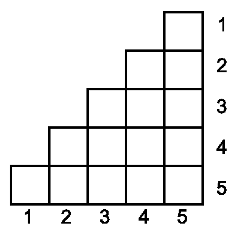
一个方阵的副对角线是指从右上角到左下角的一条对角线。我们定义 $n$ 级“楼梯”为一个 $n×n$ 的方阵，其中副对角线上方没有方格（如下图所示为 $5$ 级楼梯）。  $n$ 级楼梯的方格中站有 $m$ 个运动员。 每位运动员移动到楼梯上相邻的一个方格需要一秒钟。在比赛开始前，每位运动员都必须选择一条最短路径前往副对角线。 随着发令哨声响起，所有运动员沿各自选择的路径出发，开始移动。当运动员到达副对角线上的任意一个方格后便停止移动，不再行动。比赛在所有运动员到达副对角线后结束。如果整个过程中没有任意两名运动员在同一时刻出现在同一个方格内，则比赛是成功的。副对角线上的任意一个方格同一时刻最多只能站一名运动员。如果某一时刻，一名运动员刚刚离开某个方格，另一名运动员正好进入该方格，则他们不被认为处于同一个方格。另外，其他极端情况（比如两名运动员迎面相遇）是不可能发生的，因为运动员选择的都是最短路径。 现在给你 $m$ 位运动员在楼梯上的位置，请你从中选择最多的运动员，使得他们之间可以成功地完成比赛，即存在一种最短路径的选择方式，使得在比赛过程中，任意时刻没有两人在同一方格。 没有被选中的运动员会在比赛前被移出楼梯。

第一行包含两个整数 $n$ 和 $m$（$1 \leq n, m \leq 10^{5}$）。接下来 $m$ 行，每行包含一对整数 $r_i, c_i$（$1 \leq r_i, c_i \leq n$，且 $n - c_i < r_i$），分别表示第 $i$ 位运动员的行号和列号（具体行列编号方式见说明图片）。不存在两名运动员站在同一方格。

第一行输出可以选择的运动员最大人数。第二行输出这些被选中运动员的编号，编号按照输入顺序从 $1$ 开始。编号顺序可以任意给出，用空格分隔。如果有多组解，输出任意一组均可。

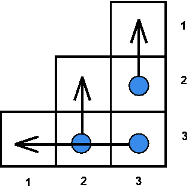
对第一个样例的说明：  图为 $3$ 级楼梯。箭头表示运动员选择的最短路径。 由 ChatGPT 5 翻译