CF1450B Balls of Steel

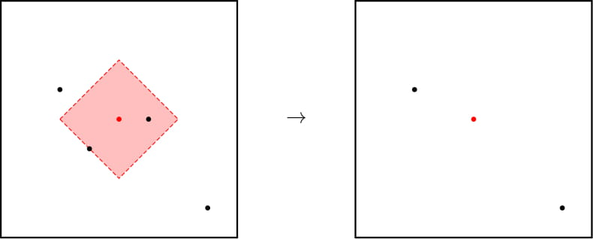
你有 $n$ 个平面上的不同点 $(x_1, y_1),\ldots,(x_n,y_n)$，以及一个非负整数参数 $k$。每个点都是一个微观钢球，$k$ 是钢球被充能时的吸引力。所有钢球的吸引力都相同。 每次操作，你可以选择一个钢球 $i$ 进行充能。被充能后，所有与钢球 $i$ 的曼哈顿距离不超过 $k$ 的钢球都会移动到钢球 $i$ 的位置。一次操作后，可能有多个钢球处于同一坐标。 更正式地说，对于所有满足 $|x_i - x_j| + |y_i - y_j| \le k$ 的钢球 $j$，我们令 $x_j := x_i$ 且 $y_j := y_i$。  一次操作的示例。充能中心的钢球后，另外两个钢球移动到它的位置。右图中，中心的红点是这些钢球的共同位置。你的任务是求出将所有钢球移动到同一位置所需的最少操作次数，或者报告这不可能实现。

第一行包含一个整数 $t$（$1 \le t \le 100$），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $n$、$k$（$2 \le n \le 100$，$0 \le k \le 10^6$），分别表示钢球的数量和所有钢球的吸引力。 接下来的 $n$ 行描述钢球的坐标。第 $i$ 行包含两个整数 $x_i$、$y_i$（$0 \le x_i, y_i \le 10^5$），表示第 $i$ 个钢球的坐标。 保证所有点互不相同。

对于每个测试用例，输出一个整数，表示将所有钢球移动到同一位置所需的最少操作次数。如果无法实现，输出 $-1$。

在第一个测试用例中，有三个钢球，坐标分别为 $(0, 0)$、$(3, 3)$ 和 $(1, 1)$，吸引力为 $2$。可以通过一次操作将两个钢球聚在一起，但无论多少次操作都无法将三个钢球聚在一起。 在第二个测试用例中，有三个钢球，坐标分别为 $(6, 7)$、$(8, 8)$ 和 $(6, 9)$，吸引力为 $3$。无论选择哪个钢球充能，其他两个都会移动到同一位置，因此只需一次操作。 在第三个测试用例中，有四个钢球，坐标分别为 $(0, 0)$、$(0, 1)$、$(0, 2)$ 和 $(0, 3)$，吸引力为 $1$。可以证明，无法通过一系列操作将所有钢球移动到同一位置。 由 ChatGPT 4.1 翻译