CF1450C1 Errich-Tac-Toe (Easy Version)

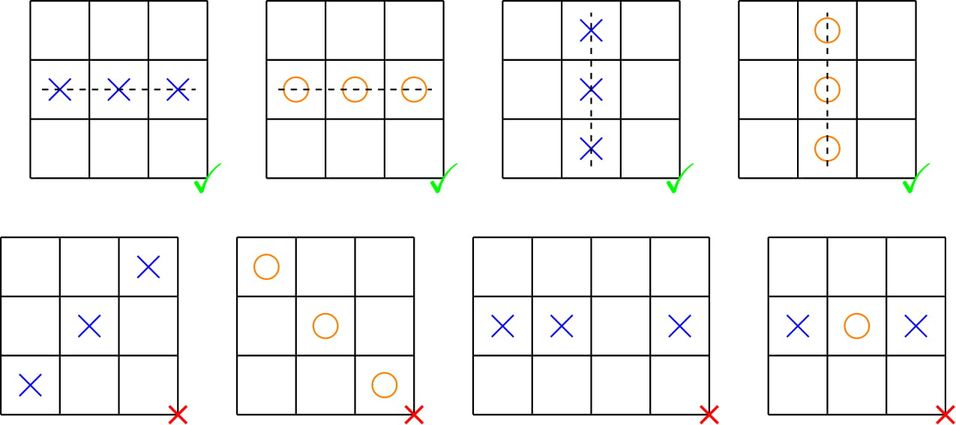
简单版与困难版的唯一区别在于，简单版的输入中不会出现 O 类型的棋子。 Errichto 给了 Monogon 如下挑战，以此来吓阻他在 Codeforces 上夺取他的顶级贡献者位置。 在一个 $n$ 行 $n$ 列的井字棋棋盘上，每个格子要么是空的，要么放有一个棋子。棋子有两种类型：X 和 O。如果某一行或某一列中存在连续三个相同类型的棋子，则该棋盘为获胜局面。否则为平局局面。  第一行中的图案为获胜局面，第二行中的图案为平局局面。 每次操作，你可以将一个 X 变为 O，或将一个 O 变为 X。设 $k$ 为棋盘上棋子的总数。你的任务是在不超过 $\lfloor \frac{k}{3}\rfloor$（向下取整）次操作内，将棋盘变为平局局面。 你不需要最小化操作次数。

第一行包含一个整数 $t$（$1\le t\le 100$），表示测试用例数量。 每个测试用例的第一行包含一个整数 $n$（$1\le n\le 300$），表示棋盘的大小。 接下来的 $n$ 行，每行包含一个长度为 $n$ 的字符串，表示初始棋盘。第 $i$ 行第 $j$ 列的字符为 '.' 表示该格为空，或为该格子的棋子类型：'X' 或 'O'。 保证并非所有格子都是空的。 在简单版中，输入中不会出现字符 'O'。 所有测试用例中 $n$ 的总和不超过 $300$。

对于每个测试用例，输出操作后的棋盘状态。 我们已证明总有解。如果有多种方案，输出任意一种即可。

在第一个测试用例中，第二行和第二列最初都有连续三个 'X'。将中间的棋子改为 'O' 后，棋盘变为平局局面，只改变了 $1\le \lfloor 5/3\rfloor$ 个棋子。 在第二个测试用例中，只需改变 $9\le \lfloor 32/3\rfloor$ 个棋子，且不存在任何一行或一列有连续三个 'X' 或 'O'，因此为平局局面。 在第三个测试用例中，只需改变 $3\le \lfloor 12/3\rfloor$ 个棋子，最终棋盘为平局局面。 由 ChatGPT 4.1 翻译