CF1450H1 Multithreading (Easy Version)

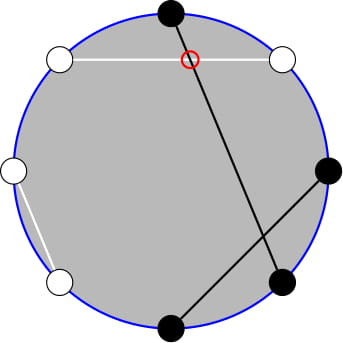
本题的两个版本唯一的区别在于，简单版中没有更新操作。 有 $n$ 个线轴均匀地放置在一个圆桌的边缘上。线轴有两种类型：一种是黑线，另一种是白线。 对于任意两个颜色相同的线轴，你可以用同色的线将它们以一条直线段连接起来。我们定义一次“匹配”为将所有线轴两两配对，使得每个线轴恰好与另一个线轴配对。 “染色”指的是给所有线轴分配颜色（白或黑）。如果某种染色下黑线轴和白线轴的数量都是偶数，则称该染色是“合法的”。也就是说，只有当黑线轴和白线轴的数量均为偶数时，才存在一种匹配方案。 给定一种匹配方式，我们可以统计白线与黑线之间的线段相交的次数。我们计算的是不同颜色的线段相交的对数，而不是交点的个数，因此如果多个不同颜色的线段在同一个点相交，这个交点会被多次计数。若 $c$ 是一种合法染色，记 $f(c)$ 为所有可能匹配方式中，不同颜色线段相交次数的最小值。  上图描述的圆圈染色为 bwbbbwww。按照图中所示的配对方式，不同颜色的线段有 1 次相交。可以证明这是最小可能值，因此 $f(\text{bwbbbwww}) = 1$。 现在给定一个字符串 $s$，表示未完成的染色方案，其中每个字符为 'w'、'b' 或 '?'，分别表示白线轴、黑线轴或未染色的线轴。 如果通过给 $s$ 中的 '?' 赋予颜色（其余位置不变），可以得到染色 $c$，则称 $c$ 是 $s$-可达的。 在所有合法且 $s$-可达的染色中，等概率随机选择一种染色 $c$。请计算 $f(c)$ 的期望值。答案需对 $998244353$ 取模。 可以证明，答案可以表示为 $\frac{p}{q}$，其中 $p$ 和 $q$ 互质，且 $q\not\equiv 0\pmod{998244353}$。最终答案为 $(p\cdot q^{-1})$ 对 $998244353$ 取模的结果。

第一行包含两个整数 $n$ 和 $m$（$2\le n\le 2\cdot 10^5$，$n$ 为偶数，$m=0$）——线轴的数量和操作次数。简单版中没有更新操作，因此 $m$ 恒为 $0$。 第二行包含一个长度为 $n$ 的字符串 $s$，表示线轴的未完成染色。第 $i$ 个字符为 'w'、'b' 或 '?'，分别表示第 $i$ 个线轴为白色、黑色或未染色。 保证至少存在一个未染色的线轴。

输出 $f(c)$ 的期望值，对 $998244353$ 取模。

第一个测试样例与图片对应。将 '?' 染为 'w' 后，黑线轴数量为奇数，不合法。因此唯一可达的合法染色为 'bwbbbwww'，且 $f(\text{bwbbbwww}) = 1$，所以期望值为 $1$。 可以证明，第二个测试样例的期望值为 $\frac{9}{16}$。 由 ChatGPT 4.1 翻译