CF1454E Number of Simple Paths
题目描述
给你一张 $ n $ 个节点 $ n $ 条边的**无向连通简单图**,请你计算出这张图中长度大于等于 $ 1 $ 的不同的**简单路径**的数量,保证图中没有自环和重边。其中,简单路径中的节点必须互不相同,一条路径的长度定义为它所包含的边的数量。
两条路径仅有方向不同时被认为是同一条,例如 $ 1 \rightarrow 2 $ 和 $ 2 \rightarrow 1 $。
输入格式
第一行一个整数 $ t ( 1 \le t \le 2 \times 10^4 ) $,表示数据组数。
每组数据中,第一行是一个整数 $ n ( 3 \le n \le 2 \times 10^5 ) $,表示图的节点数和边数。接下来 $ n $ 行,每行两个整数 $ u , v $,表示一条无向边。
输出格式
对每组数据输出一个整数,表示不同的简单路径的数量。
数据保证所有的 $ n $ 之和不超过 $ 2 \times 10 ^ 5 $。
说明/提示
Consider the second test case of the example. It looks like that:
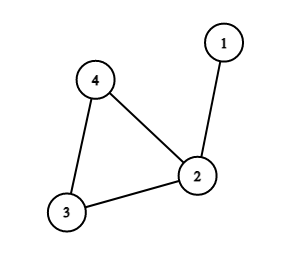
There are $ 11 $ different simple paths:
1. $ [1, 2] $ ;
2. $ [2, 3] $ ;
3. $ [3, 4] $ ;
4. $ [2, 4] $ ;
5. $ [1, 2, 4] $ ;
6. $ [1, 2, 3] $ ;
7. $ [2, 3, 4] $ ;
8. $ [2, 4, 3] $ ;
9. $ [3, 2, 4] $ ;
10. $ [1, 2, 3, 4] $ ;
11. $ [1, 2, 4, 3] $ .