CF1455E Four Points

给定平面直角坐标系上的四个不同的整点 $p_1$、$p_2$、$p_3$ 和 $p_4$。 每一步，你可以选择其中一个点 $p_i$，并将其沿四个方向之一移动一个单位。换句话说，如果你选择了点 $p_i = (x, y)$，你可以将其移动到 $(x, y+1)$、$(x, y-1)$、$(x+1, y)$ 或 $(x-1, y)$。 你的目标是通过移动这些点，使它们最终形成一个边平行于 $OX$ 轴和 $OY$ 轴的正方形（允许边长为 $0$ 的正方形）。 你需要求出最少需要多少步才能使这四个点形成这样的正方形。

第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例包含四行，每行包含两个整数 $x$ 和 $y$（$0 \le x, y \le 10^9$），表示一个点 $p_i = (x, y)$ 的坐标。 每个测试用例中的四个点均不相同。

对于每个测试用例，输出一个整数，表示使四个点形成正方形所需的最小步数。

在第一个测试用例中，一种最优方案如下所示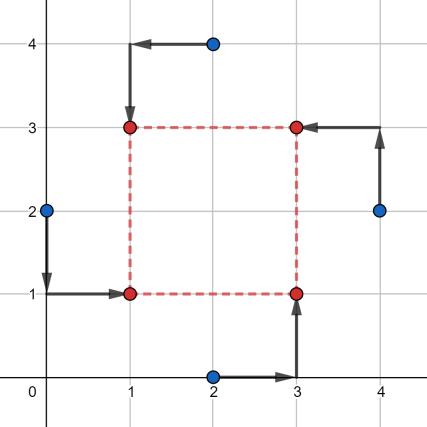：  每个点都移动了两次，所以答案为 $2 + 2 + 2 + 2 = 8$。 在第二个测试用例中，一种最优方案如下所示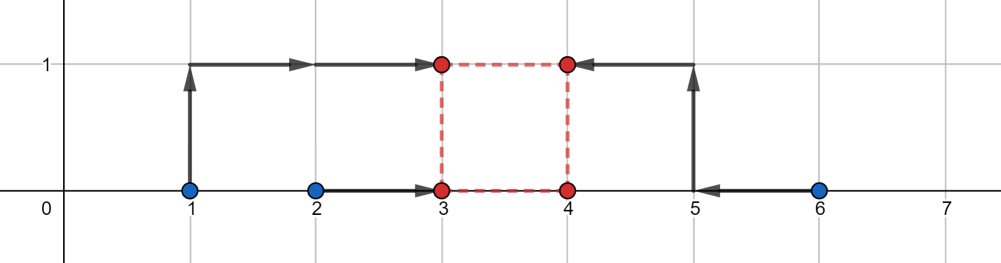：  答案为 $3 + 1 + 0 + 3 = 7$。 在第三个测试用例中，一种最优方案如下所示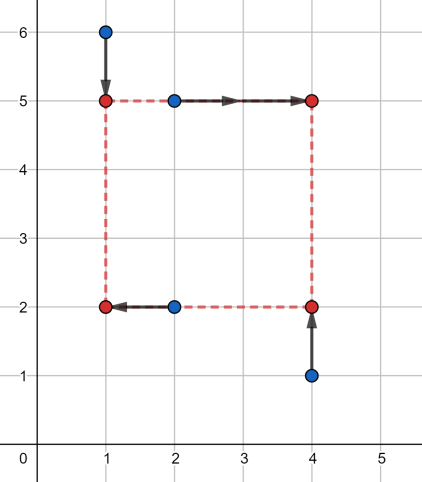：  答案为 $1 + 1 + 2 + 1 = 5$。 由 ChatGPT 4.1 翻译