CF1455E Four Points

You are given four different integer points $ p_1 $ , $ p_2 $ , $ p_3 $ and $ p_4 $ on $ \mathit{XY} $ grid. In one step you can choose one of the points $ p_i $ and move it in one of four directions by one. In other words, if you have chosen point $ p_i = (x, y) $ you can move it to $ (x, y + 1) $ , $ (x, y - 1) $ , $ (x + 1, y) $ or $ (x - 1, y) $ . Your goal to move points in such a way that they will form a square with sides parallel to $ \mathit{OX} $ and $ \mathit{OY} $ axes (a square with side $ 0 $ is allowed). What is the minimum number of steps you need to make such a square?

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. Each test case consists of four lines. Each line contains two integers $ x $ and $ y $ ( $ 0 \le x, y \le 10^9 $ ) — coordinates of one of the points $ p_i = (x, y) $ . All points are different in one test case.

For each test case, print the single integer — the minimum number of steps to make a square.

In the first test case, one of the optimal solutions is shown below: 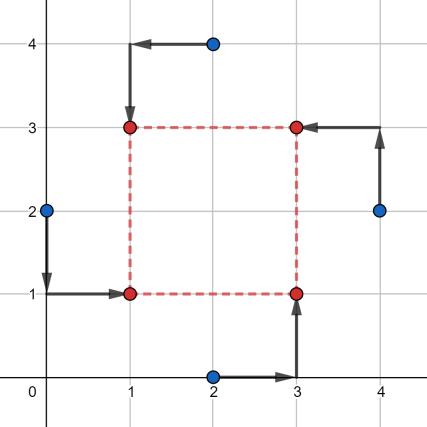 Each point was moved two times, so the answer $ 2 + 2 + 2 + 2 = 8 $ .In the second test case, one of the optimal solutions is shown below: 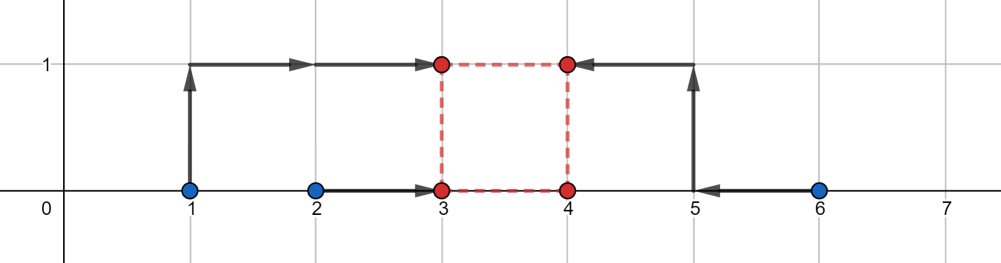 The answer is $ 3 + 1 + 0 + 3 = 7 $ .In the third test case, one of the optimal solutions is shown below: 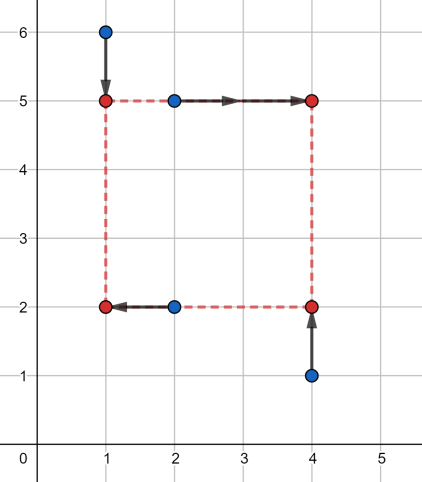 The answer is $ 1 + 1 + 2 + 1 = 5 $ .