CF1466D 13th Labour of Heracles

你可能听说过赫拉克勒斯的十二项任务，但你知道第十三项吗？人们普遍认为他花了十二年完成这十二项壮举，平均每年完成一项。如今时光流转得更快，你只有几分钟而不是几个月来完成这个任务。你能做到吗？ 本题中，给定一棵有 $n$ 个带权顶点的树。树是一个包含 $n-1$ 条边的连通图。 我们定义其 $k$ 染色为：将 $k$ 种颜色分配给树的边，使得每条边恰好被分配一种颜色。注意，你不必使用所有 $k$ 种颜色。 对于颜色 $x$ 的子图，包含原树中被分配为颜色 $x$ 的所有边，以及所有与这些边相连的顶点（即这些顶点的度数不为 $0$）。因此，子图中没有度数为 $0$ 的顶点。 一个连通分量的价值定义为其所有顶点权值之和。一个子图的价值定义为其所有连通分量价值的最大值。我们约定空子图的价值为 $0$。 $k$ 染色的价值定义为所有 $k$ 种颜色对应子图的价值之和。给定一棵树，对于每个 $k$ 从 $1$ 到 $n-1$，计算该树的最大 $k$ 染色价值。

输入的第一行包含一个整数 $t$（$1 \leq t \leq 10^5$），表示测试用例的数量。接下来是 $t$ 个测试用例。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 10^5$）。第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$（$0 \leq w_i \leq 10^9$），其中 $w_i$ 表示第 $i$ 个顶点的权值。接下来的 $n-1$ 行，每行包含两个整数 $u, v$（$1 \leq u, v \leq n$），表示顶点 $u$ 和 $v$ 之间有一条边。保证这些边构成一棵树。 所有测试用例中 $n$ 的总和不超过 $2 \times 10^5$。

对于每个测试用例，输出一行，包含 $n-1$ 个整数，用空格隔开。第 $i$ 个数表示该树的最大 $i$ 染色价值。

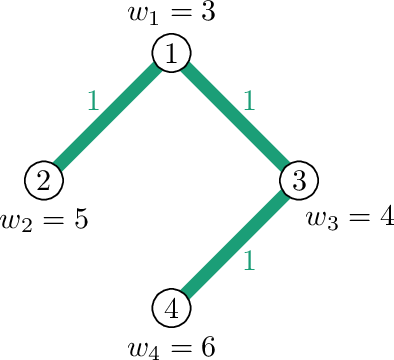
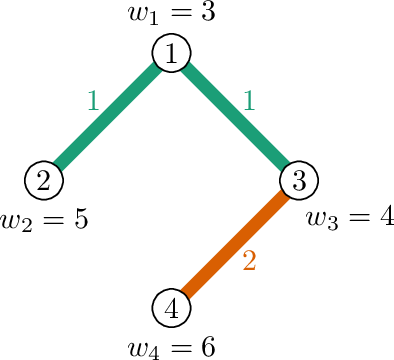
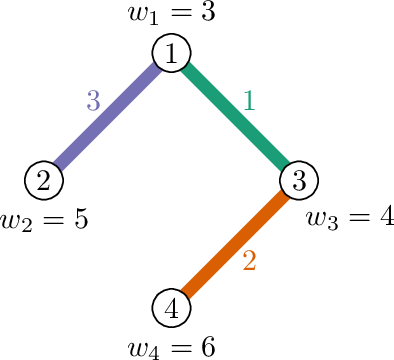
第一个测试用例的最优染色方案如下：  在 $1$ 染色中，所有边都被赋予相同的颜色。颜色 $1$ 的子图包含原图的所有边和顶点，因此其价值为 $3+5+4+6=18$。  在最优的 $2$ 染色中，边 $(2,1)$ 和 $(3,1)$ 被赋予颜色 $1$，边 $(4,3)$ 被赋予颜色 $2$。因此，颜色 $1$ 的子图是一个连通分量（顶点 $1,2,3$），其价值为 $3+5+4=12$。颜色 $2$ 的子图包含两个顶点和一条边，其价值为 $4+6=10$。  在最优的 $3$ 染色中，所有边都被赋予不同的颜色。因此，每种颜色的子图都只包含一条边。它们的价值分别为：$3+4=7$，$4+6=10$，$3+5=8$。 由 ChatGPT 4.1 翻译