CF1468G Hobbits

霍比特人 Frodo 和 Sam 正携带至尊魔戒前往 Mordor。为了不被兽人发现，他们决定穿越山脉。 山脉的地形可以用一条由 $n$ 个点 $ (x_i, y_i) $ 构成的折线表示，点的编号从 $1$ 到 $n$（对于 $1 \le i \le n - 1$，有 $x_i < x_{i+1}$）。霍比特人从点 $ (x_1, y_1) $ 出发，必须到达点 $ (x_n, y_n) $ 才能完成任务。 问题在于，索伦之眼所在的高塔正注视着他们。高塔位于点 $ (x_n, y_n) $，高度为 $H$，因此索伦之眼的位置为 $ (x_n, y_n + H) $。为了顺利完成任务，霍比特人必须在被索伦之眼看到时全程穿上斗篷，也就是说，当从索伦之眼到霍比特人的直线没有被地形阻挡时，他们就会被看到。 霍比特人身高很矮，可以认为他们的高度可以忽略不计，但仍为正数，所以当从索伦之眼到霍比特人的直线仅与地形相切时，索伦之眼依然可以看到他们。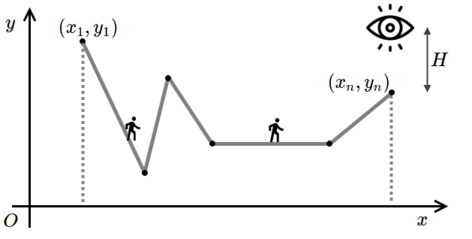  当霍比特人在左侧位置时，索伦之眼看不到他们；在右侧位置时，索伦之眼可以看到他们。霍比特人不喜欢穿斗篷，所以他们只在被索伦之眼看到时才穿。你的任务是计算霍比特人需要穿斗篷行走的总距离。

输入的第一行包含两个整数 $n$ 和 $H$（$2 \le n \le 2 \cdot 10^5$，$1 \le H \le 10^4$），分别表示折线的顶点数和高塔的高度。 接下来的 $n$ 行，每行包含两个整数 $x_i, y_i$（$0 \le x_i \le 4 \cdot 10^5$，$0 \le y_i \le 10^4$），表示折线顶点的坐标。保证对于 $1 \le i \le n-1$，有 $x_i < x_{i+1}$。

输出一个实数，表示霍比特人需要穿斗篷行走的总距离。你的答案将被认为是正确的，当且仅当其绝对误差或相对误差不超过 $10^{-6}$。即，若你的答案为 $a$，标准答案为 $b$，则当 $\dfrac{|a - b|}{\max(1, b)} \le 10^{-6}$ 时，答案被接受。

由 ChatGPT 4.1 翻译