CF1468J Road Reform
题目描述
在 Berland 有 $n$ 个城市和 $m$ 条双向道路。第 $i$ 条道路连接城市 $x_i$ 和 $y_i$,限速为 $s_i$。该道路网络保证任意两个城市之间都可以互相到达。
Berland 交通部计划进行道路改革。
首先,维护所有 $m$ 条道路的成本太高,因此将拆除 $m - (n - 1)$ 条道路,使得剩下的 $(n - 1)$ 条道路依然保证任意两个城市之间可以互相到达。形式上,剩下的道路应构成一棵无向树。
其次,剩余道路的限速可以调整。每次调整可以将某条道路的限速加 $1$ 或减 $1$。由于调整限速的工作量很大,交通部希望最小化调整次数。
交通部的目标是让剩下的 $(n - 1)$ 条道路中,所有道路的最大限速恰好等于 $k$。你的任务是计算,为了满足要求,最少需要多少次限速调整。
例如,假设初始地图如下,$k = 7$:
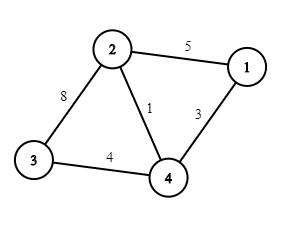
一种最优方案是拆除道路 $1$–$4$ 和 $3$–$4$,然后将道路 $2$–$3$ 的限速减少 $1$,最终道路网络如下:
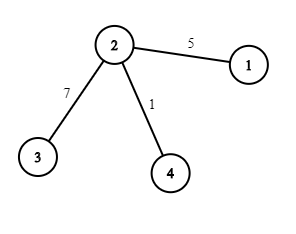
输入格式
第一行包含一个整数 $t$($1 \le t \le 1000$),表示测试用例数量。
每个测试用例的第一行包含三个整数 $n$、$m$ 和 $k$($2 \le n \le 2 \cdot 10^5$;$n-1 \le m \le \min(2 \cdot 10^5, \frac{n(n-1)}{2})$;$1 \le k \le 10^9$),分别表示城市数、道路数和要求的最大限速。
接下来 $m$ 行,每行三个整数 $x_i$、$y_i$ 和 $s_i$($1 \le x_i, y_i \le n$;$x_i \ne y_i$;$1 \le s_i \le 10^9$),表示第 $i$ 条道路连接的城市和限速。所有道路都是双向的。
每个测试用例中的道路网络都是连通的(即任意两个城市之间都可以通过道路到达),且每对城市之间至多有一条道路。
所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$,$m$ 的总和也不超过 $2 \cdot 10^5$。
输出格式
对于每个测试用例,输出一个整数,表示交通部为满足要求最少需要进行多少次限速调整。
说明/提示
示例测试的解释:
第一个测试用例已在题目描述中说明。
第二个测试用例,初始道路网络如下:
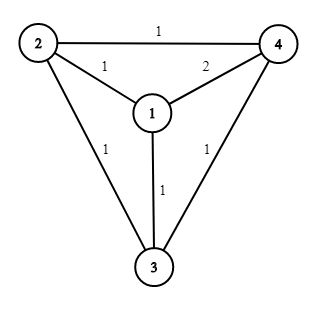
交通部可以拆除道路 $1$–$2$、$3$–$2$ 和 $3$–$4$,然后将道路 $1$–$4$ 的限速增加三次。
第三个测试用例,道路网络已经满足所有要求。
第四个测试用例,只需拆除道路 $1$–$2$,剩余道路网络即可满足要求。
由 ChatGPT 4.1 翻译