CF1469F Power Sockets

定义一条链： - 长度为 $1$ 的链是一个单独的顶点； - 长度为 $x$ 的链是在长度为 $x-1$ 的链的末端连接一个新顶点，并用一条边相连。 给定 $n$ 条长度分别为 $l_1, l_2, \dots, l_n$ 的链。你计划用其中一些链来构建一棵树。 - 树中的每个顶点要么是白色，要么是黑色。 - 树最初只有一个白色的根节点。 - 所有链最初都只包含白色顶点。 - 你可以选择一条链，将其任意一个顶点与树中的任意一个白色顶点用一条边连接。该链成为树的一部分。连接这条边的两个端点都会变成黑色。 - 每条链最多只能使用一次。 - 有些链可以不使用。 树中两个顶点之间的距离定义为它们之间最短路径上的边数。 如果最终树中至少有 $k$ 个白色顶点，则树的价值为根节点到第 $k$ 近的白色顶点的距离。 你能获得的最小树的价值是多少？如果无法构建一棵包含至少 $k$ 个白色顶点的树，则输出 $-1$。

第一行包含两个整数 $n$ 和 $k$（$1 \le n \le 2 \times 10^5$，$2 \le k \le 10^9$），分别表示链的数量和树中至少需要的白色顶点数。 第二行包含 $n$ 个整数 $l_1, l_2, \dots, l_n$（$3 \le l_i \le 2 \times 10^5$），表示每条链的长度。

输出一个整数。如果无法构建一棵包含至少 $k$ 个白色顶点的树，输出 $-1$；否则，输出树可能的最小价值。

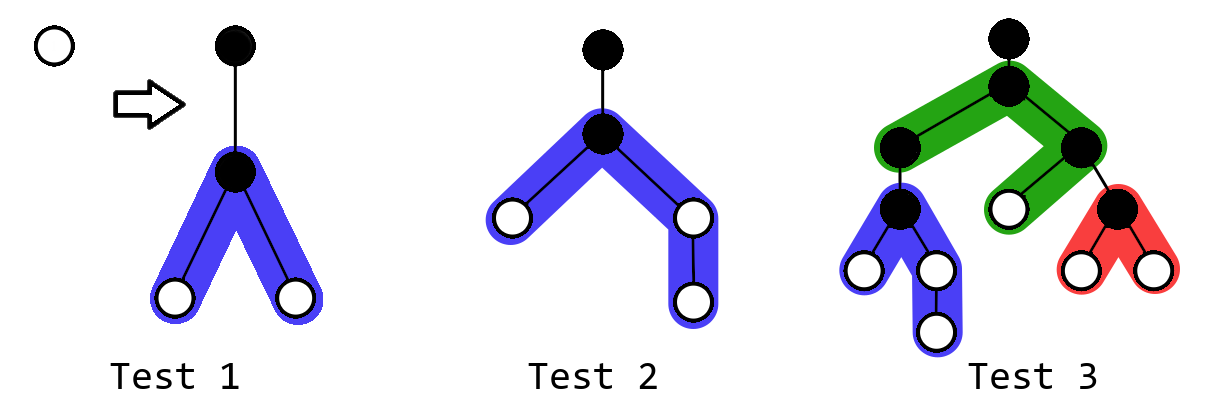你可以选择不使用所有的链，因此在第二个样例中，只使用长度为 $4$ 的链是最优的。 由 ChatGPT 4.1 翻译