CF1473G Tiles

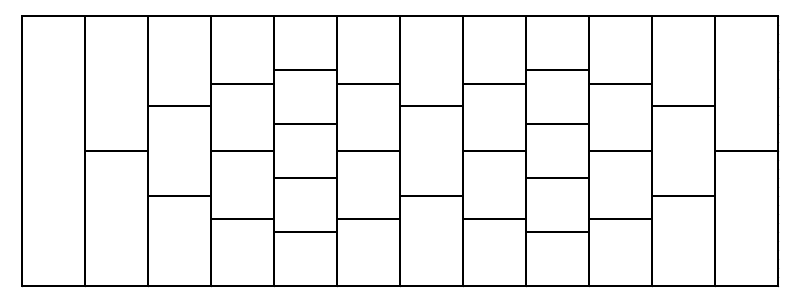
考虑一条由多行组成的道路。每一行被划分为若干个矩形瓷砖，并且同一行内的所有瓷砖都是相同的。第一行恰好包含一个矩形瓷砖。请参考下图，图中展示了瓷砖的排列方式。 道路的构建方式如下： - 第一行包含 $1$ 个瓷砖； - 接下来有 $a_1$ 行，每一行比前一行多 $1$ 个瓷砖； - 然后有 $b_1$ 行，每一行比前一行少 $1$ 个瓷砖； - 接着有 $a_2$ 行，每一行比前一行多 $1$ 个瓷砖； - 然后有 $b_2$ 行，每一行比前一行少 $1$ 个瓷砖； - ... - 然后有 $a_n$ 行，每一行比前一行多 $1$ 个瓷砖； - 最后有 $b_n$ 行，每一行比前一行少 $1$ 个瓷砖。  上图是 $n=2$，$a_1=4$，$b_1=2$，$a_2=2$，$b_2=3$ 的道路示例。各行从左到右排列。你从第一行唯一的瓷砖出发，目标是到达最后一行（可以到达最后一行的任意一个瓷砖）。从当前瓷砖，你可以移动到下一行中与当前瓷砖相邻的任意瓷砖。 请计算从第一行到最后一行的不同路径数。由于答案可能很大，请输出对 $998244353$ 取模后的结果。

第一行包含一个整数 $n$（$1 \le n \le 1000$）。 接下来有 $n$ 行，第 $i$ 行包含两个整数 $a_i$ 和 $b_i$（$1 \le a_i, b_i \le 10^5$；$|a_i - b_i| \le 5$）。 输入的额外约束：$a_i$ 和 $b_i$ 的序列不会导致某一行的瓷砖数为非正数。

输出一个整数，表示从第一行到最后一行的路径数，对 $998244353$ 取模。

由 ChatGPT 4.1 翻译