CF1476C Longest Simple Cycle

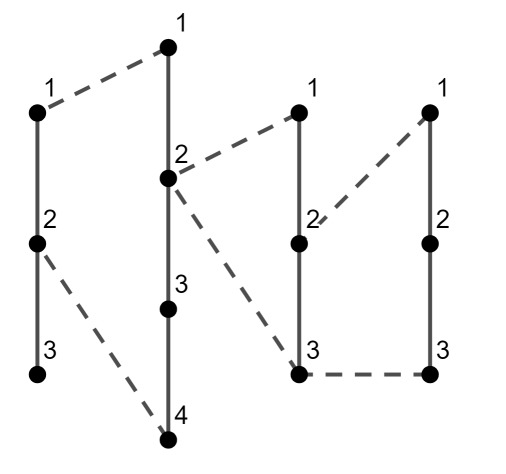
你有 $n$ 条链，第 $i$ 条链包含 $c_i$ 个顶点。每条链上的顶点编号独立，从 $1$ 到 $c_i$。换句话说，第 $i$ 条链是一个有 $c_i$ 个顶点的无向图，且有 $c_i-1$ 条边，分别连接第 $j$ 个顶点和第 $j+1$ 个顶点（$1 \le j < c_i$）。 现在你决定按如下方式将这些链合并成一个图： 1. 跳过第一条链； 2. 将第 $i$ 条链的第 $1$ 个顶点与第 $i-1$ 条链的第 $a_i$ 个顶点连接一条边； 3. 将第 $i$ 条链的最后一个（第 $c_i$ 个）顶点与第 $i-1$ 条链的第 $b_i$ 个顶点连接一条边。  上图为第一个测试用例的示意图。虚线为合并过程中添加的边。 请计算合并后所得图中最长的简单环的长度。 一个简单环是指首尾相连的链，且在环上每个顶点只访问一次。

第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 10^5$），表示链的数量。 每个测试用例的第二行包含 $n$ 个整数 $c_1, c_2, \dots, c_n$（$2 \le c_i \le 10^9$），表示每条链上的顶点数。 每个测试用例的第三行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$（$a_1 = -1$，$1 \le a_i \le c_{i-1}$）。 每个测试用例的第四行包含 $n$ 个整数 $b_1, b_2, \dots, b_n$（$b_1 = -1$，$1 \le b_i \le c_{i-1}$）。 保证 $a_1$ 和 $b_1$ 都等于 $-1$，它们不会用于建图，仅用于下标对齐。保证所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每个测试用例，输出合并后所得图中最长简单环的长度。

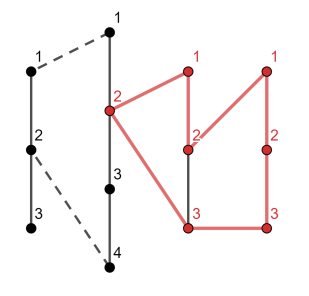
在第一个测试用例中，最长的简单环如下图所示：  无法通过第一条链增加环的长度，否则就不是简单环了——第二条链上的顶点 $2$ 会被重复访问。 由 ChatGPT 4.1 翻译