CF1486E Paired Payment

有 $n$ 个城市和 $m$ 条双向道路，这些道路构成了一个无向带权图。该图不保证连通。每条道路都有其参数 $w$。你可以通过这些道路旅行，但政府出台了一项新规定：你每次只能连续经过两条道路（即从城市 $a$ 到城市 $b$，再从城市 $b$ 到城市 $c$），并且你需要为这两条道路支付 $(w_{ab} + w_{bc})^2$ 的费用。请你判断是否可以从城市 $1$ 到达每一个其他城市 $t$，并求出从 $1$ 到 $t$ 的最小花费。

第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 10^5$，$1 \leq m \leq \min(\frac{n \cdot (n - 1)}{2}, 2 \cdot 10^5)$）。 接下来的 $m$ 行，每行包含三个整数 $v_i$、$u_i$、$w_i$（$1 \leq v_i, u_i \leq n$，$1 \leq w_i \leq 50$，$u_i \neq v_i$）。保证没有重边，即对于任意一条边 $(u_i, v_i)$，不存在另一条边 $(u_i, v_i)$ 或 $(v_i, u_i)$。

对于每个城市 $t$，输出一个整数。如果不存在从 $1$ 到 $t$ 的合法路径，输出 $-1$；否则输出从 $1$ 到 $t$ 的最小花费。

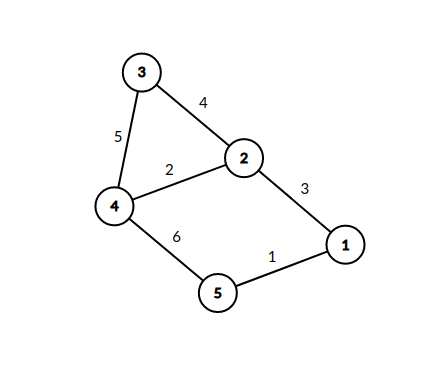
第一个样例的图如下所示。  在第二个样例中，从 $1$ 到 $3$ 的路径经过 $2$，因此费用为 $(1 + 2)^2 = 9$。  由 ChatGPT 4.1 翻译