CF1486E Paired Payment

There are $ n $ cities and $ m $ bidirectional roads in the country. The roads in the country form an undirected weighted graph. The graph is not guaranteed to be connected. Each road has it's own parameter $ w $ . You can travel through the roads, but the government made a new law: you can only go through two roads at a time (go from city $ a $ to city $ b $ and then from city $ b $ to city $ c $ ) and you will have to pay $ (w_{ab} + w_{bc})^2 $ money to go through those roads. Find out whether it is possible to travel from city $ 1 $ to every other city $ t $ and what's the minimum amount of money you need to get from $ 1 $ to $ t $ .

First line contains two integers $ n $ , $ m $ ( $ 2 \leq n \leq 10^5 $ , $ 1 \leq m \leq min(\frac{n \cdot (n - 1)}{2}, 2 \cdot 10^5) $ ). Next $ m $ lines each contain three integers $ v_i $ , $ u_i $ , $ w_i $ ( $ 1 \leq v_i, u_i \leq n $ , $ 1 \leq w_i \leq 50 $ , $ u_i \neq v_i $ ). It's guaranteed that there are no multiple edges, i.e. for any edge $ (u_i, v_i) $ there are no other edges $ (u_i, v_i) $ or $ (v_i, u_i) $ .

For every city $ t $ print one integer. If there is no correct path between $ 1 $ and $ t $ output $ -1 $ . Otherwise print out the minimum amount of money needed to travel from $ 1 $ to $ t $ .

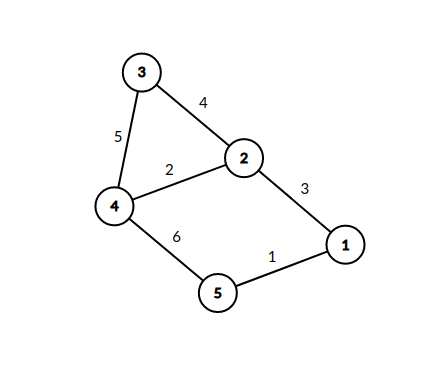
The graph in the first example looks like this.  In the second example the path from $ 1 $ to $ 3 $ goes through $ 2 $ , so the resulting payment is $ (1 + 2)^2 = 9 $ .