CF1486F Pairs of Paths

You are given a tree consisting of $ n $ vertices, and $ m $ simple vertex paths. Your task is to find how many pairs of those paths intersect at exactly one vertex. More formally you have to find the number of pairs $ (i, j) $ $ (1 \leq i < j \leq m) $ such that $ path_i $ and $ path_j $ have exactly one vertex in common.

First line contains a single integer $ n $ $ (1 \leq n \leq 3 \cdot 10^5) $ . Next $ n - 1 $ lines describe the tree. Each line contains two integers $ u $ and $ v $ $ (1 \leq u, v \leq n) $ describing an edge between vertices $ u $ and $ v $ . Next line contains a single integer $ m $ $ (1 \leq m \leq 3 \cdot 10^5) $ . Next $ m $ lines describe paths. Each line describes a path by it's two endpoints $ u $ and $ v $ $ (1 \leq u, v \leq n) $ . The given path is all the vertices on the shortest path from $ u $ to $ v $ (including $ u $ and $ v $ ).

Output a single integer — the number of pairs of paths that intersect at exactly one vertex.

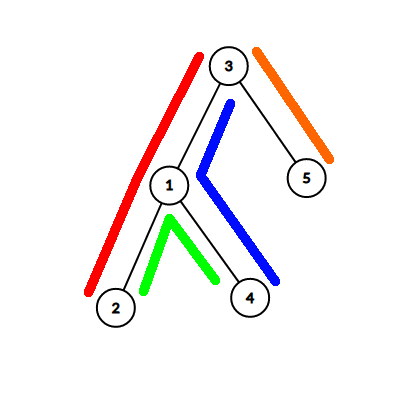
 The tree in the first example and paths look like this. Pairs $ (1,4) $ and $ (3,4) $ intersect at one vertex. In the second example all three paths contain the same single vertex, so all pairs $ (1, 2) $ , $ (1, 3) $ and $ (2, 3) $ intersect at one vertex. The third example is the same as the first example with two additional paths. Pairs $ (1,4) $ , $ (1,5) $ , $ (2,5) $ , $ (3,4) $ , $ (3,5) $ , $ (3,6) $ and $ (5,6) $ intersect at one vertex.