CF1490D Permutation Transformation

一个排列是指长度为 $n$ 的整数序列，序列中的数字从 $1$ 到 $n$，且每个数字恰好出现一次。例如，$[1]$、$[3, 5, 2, 1, 4]$、$[1, 3, 2]$ 都是排列，而 $[2, 3, 2]$、$[4, 3, 1]$、$[0]$ 不是排列。 Polycarp 最近收到了一个长度为 $n$ 的排列 $a[1 \dots n]$ 作为礼物。Polycarp 更喜欢树而不是排列，因此他想把排列 $a$ 转换成一棵有根二叉树。他将一个由不同整数构成的数组转换为树的方法如下： - 数组中的最大元素成为树的根节点； - 最大值左侧的所有元素构成左子树（对子数组左半部分递归应用同样的规则），如果最大值左侧没有元素，则根节点没有左儿子； - 最大值右侧的所有元素构成右子树（对子数组右半部分递归应用同样的规则），如果最大值右侧没有元素，则根节点没有右儿子。 例如，如果他用排列 $a=[3, 5, 2, 1, 4]$ 构建树，则根节点为 $a_2=5$，左子树为对子数组 $a[1 \dots 1]=[3]$ 构建的树，右子树为对子数组 $a[3 \dots 5]=[2, 1, 4]$ 构建的树。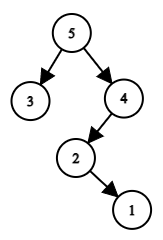最终构建出的树如下图所示：  对应排列 $a=[3, 5, 2, 1, 4]$ 的树。 另一个例子：排列为 $a=[1, 3, 2, 7, 5, 6, 4]$。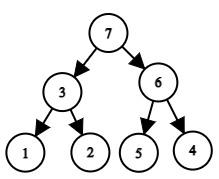此时树的结构如下：  对应排列 $a=[1, 3, 2, 7, 5, 6, 4]$ 的树。 我们用 $d_v$ 表示顶点 $a_v$ 的深度，即从根节点到编号为 $a_v$ 的顶点的路径上的边数。注意根节点的深度为 $0$。给定排列 $a$，请你求出每个顶点的 $d_v$ 值。

第一行包含一个整数 $t$（$1 \le t \le 100$），表示测试用例的数量。接下来有 $t$ 组测试用例。 每组测试用例的第一行包含一个整数 $n$（$1 \le n \le 100$），表示排列的长度。 接下来一行包含 $n$ 个数 $a_1, a_2, \ldots, a_n$，表示排列 $a$。

对于每个测试用例，输出 $n$ 个值，分别为 $d_1, d_2, \ldots, d_n$。

由 ChatGPT 4.1 翻译