Minimal Cost

## 题目描述 给你一个 $n$ 行 $10^6+2$ 列的图，行从 $1$ 到 $n$ 标号，列从 $0$ 到 $10^6+1$ 标号。 为简便，下面用 $(i,j)$ 表示第 $i$ 行第 $j$ 列的节点。 一开始每一行 $i$ 都恰好有一个障碍物 $(i,a_i)$。你可以将障碍物移动到四周空的节点（不能移出图的范围），上下移动一个单位花费 $u$，左右移动一个单位花费 $v$。（可参照上图） 你需要使得 $(1,0)$ 到 $(n,10^6+1)$ 之间有一条路径（只能上下左右移动，不能越过障碍物），求移动障碍物的最小花费。 ## 输入格式 第一行为数据组数 $t$ ($1 \leq t \leq 10^4$)。 每组数据第一行为三个整数 $n,u,v$ ($2 \leq n \leq 100, 1 \leq u,v \leq 10^9$) —— 图的行数、上下移动一个单位的花费、左右移动一个单位的花费 每组数据第二行为 $n$ 个整数 $a_1,a_2,...,a_n$ ($1 \leq a_i \leq 10^6$) —— $a_i$ 表示第 $i$ 行有障碍物 $(i,a_i)$。 保证 $\sum n \leq 2 \cdot 10^4$ ## 输出格式 对于每组数据，输出一个整数 —— 移动障碍物的最小花费。 显然在题目限制下，必然有解。

There is a graph of $ n $ rows and $ 10^6 + 2 $ columns, where rows are numbered from $ 1 $ to $ n $ and columns from $ 0 $ to $ 10^6 + 1 $ : Let's denote the node in the row $ i $ and column $ j $ by $ (i, j) $ . Initially for each $ i $ the $ i $ -th row has exactly one obstacle — at node $ (i, a_i) $ . You want to move some obstacles so that you can reach node $ (n, 10^6+1) $ from node $ (1, 0) $ by moving through edges of this graph (you can't pass through obstacles). Moving one obstacle to an adjacent by edge free node costs $ u $ or $ v $ coins, as below: - If there is an obstacle in the node $ (i, j) $ , you can use $ u $ coins to move it to $ (i-1, j) $ or $ (i+1, j) $ , if such node exists and if there is no obstacle in that node currently. - If there is an obstacle in the node $ (i, j) $ , you can use $ v $ coins to move it to $ (i, j-1) $ or $ (i, j+1) $ , if such node exists and if there is no obstacle in that node currently. - Note that you can't move obstacles outside the grid. For example, you can't move an obstacle from $ (1,1) $ to $ (0,1) $ . Refer to the picture above for a better understanding. Now you need to calculate the minimal number of coins you need to spend to be able to reach node $ (n, 10^6+1) $ from node $ (1, 0) $ by moving through edges of this graph without passing through obstacles.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains three integers $ n $ , $ u $ and $ v $ ( $ 2 \le n \le 100 $ , $ 1 \le u, v \le 10^9 $ ) — the number of rows in the graph and the numbers of coins needed to move vertically and horizontally respectively. The second line of each test case contains $ n $ integers $ a_1, a_2, \dots, a_n $ ( $ 1 \le a_i \le 10^6 $ ) — where $ a_i $ represents that the obstacle in the $ i $ -th row is in node $ (i, a_i) $ . It's guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 2 \cdot 10^4 $ .

For each test case, output a single integer — the minimal number of coins you need to spend to be able to reach node $ (n, 10^6+1) $ from node $ (1, 0) $ by moving through edges of this graph without passing through obstacles. It can be shown that under the constraints of the problem there is always a way to make such a trip possible.

3
2 3 4
2 2
2 3 4
3 2
2 4 3
3 2

7
3
3

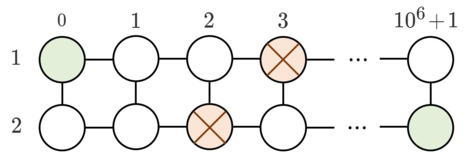
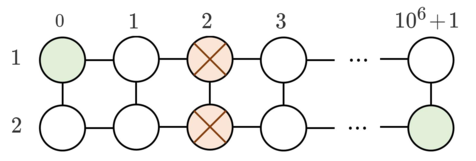In the first sample, two obstacles are at $ (1, 2) $ and $ (2,2) $ . You can move the obstacle on $ (2, 2) $ to $ (2, 3) $ , then to $ (1, 3) $ . The total cost is $ u+v = 7 $ coins. In the second sample, two obstacles are at $ (1, 3) $ and $ (2,2) $ . You can move the obstacle on $ (1, 3) $ to $ (2, 3) $ . The cost is $ u = 3 $ coins.