CF1493B Planet Lapituletti

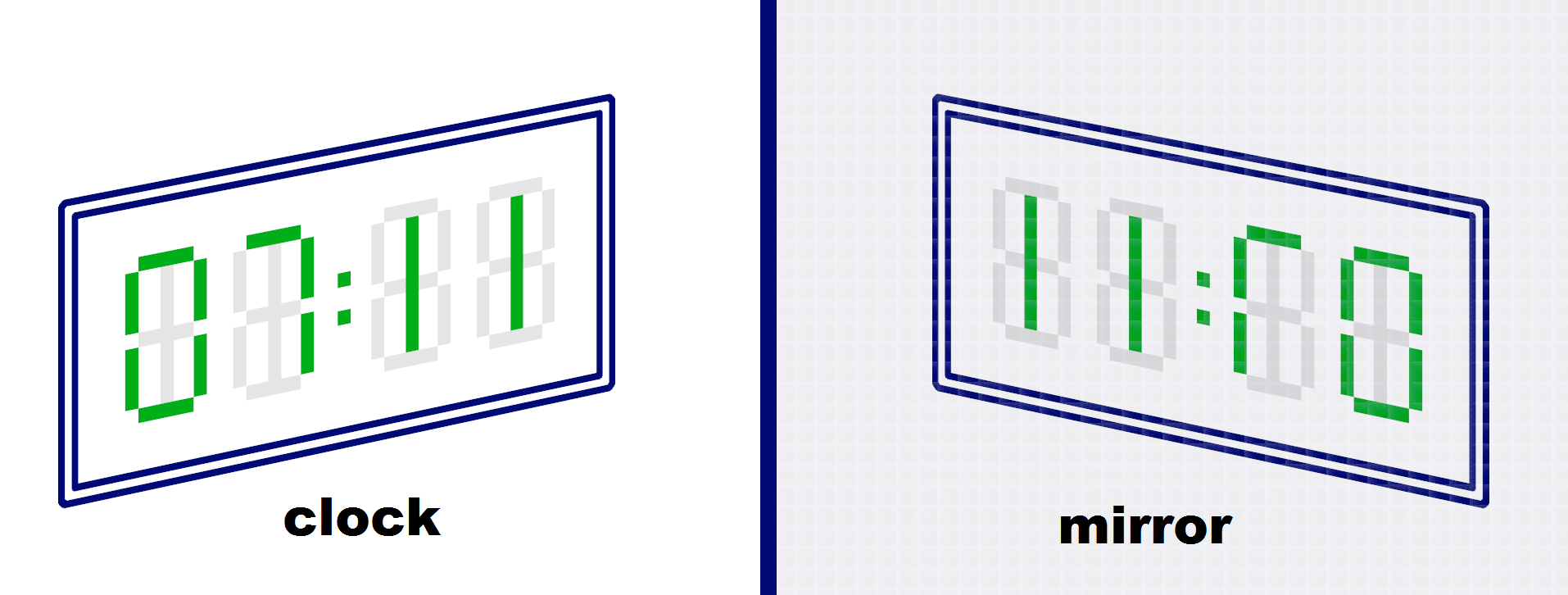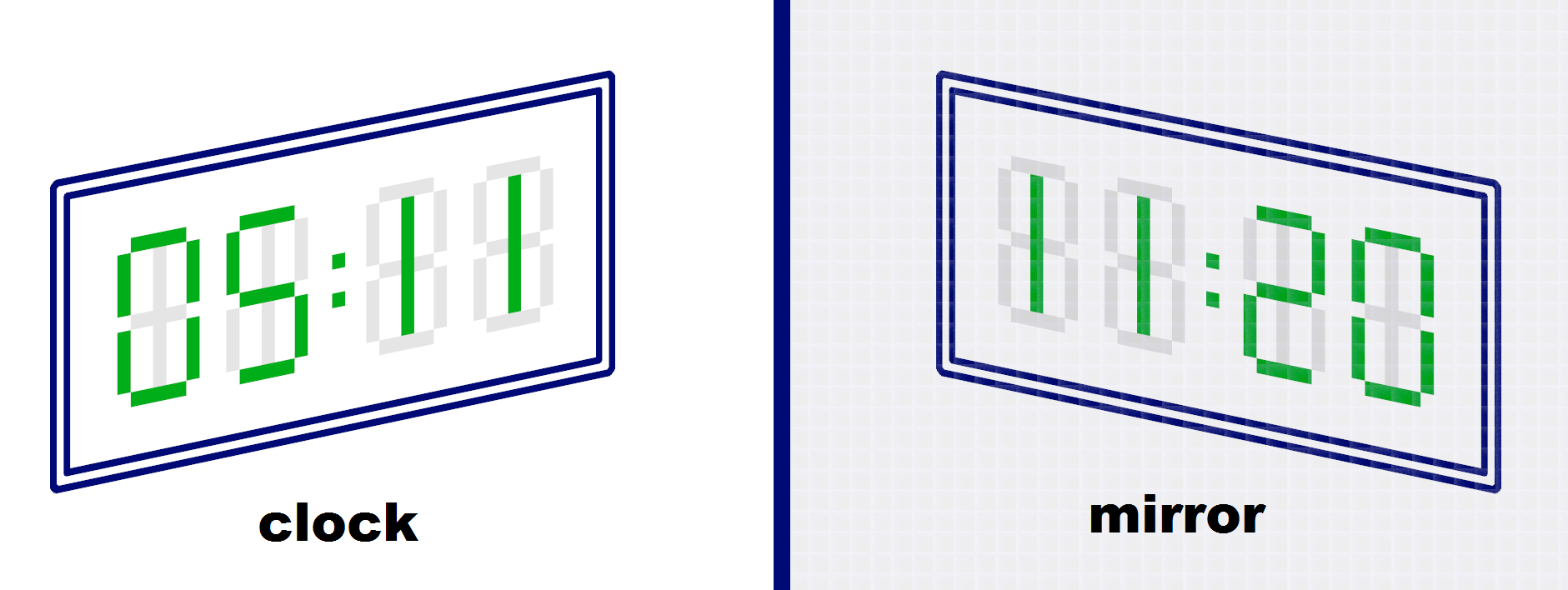
在 Lapituletti 星球上，时间的流逝方式与地球相同，但一天有 $h$ 小时，每小时有 $m$ 分钟。该星球的居民使用与地球类似的数字时钟。时钟以 HH:MM 的格式显示时间（先显示十进制的小时数，然后是冒号，接着是十进制的分钟数；如果小时或分钟不足两位，则在前面补零）。小时的编号从 $0$ 到 $h-1$，分钟的编号从 $0$ 到 $m-1$。  这是时钟上数字的显示方式。请注意，数字 $1$ 位于其位置的中间。 Lapituletti 星球上使用标准的镜子。居民们经常看着数字时钟在镜子中的倒影，并且当镜像中的时间也是一个有效时间（即镜像中的数字有效，并且该时间在一天中的某一时刻可以在正常时钟上显示）时，他们会感到高兴。 时钟在镜子中的倒影是沿垂直轴反射的。  这个倒影不是一个有效时间。  这个倒影在 $h=24$，$m=60$ 时是一个有效时间。然而，例如，如果 $h=10$，$m=60$，则这个倒影不是一个有效时间。 Lapituletti 星球上的一位居民在某个时刻 $s$ 开始观察时钟在镜子中的倒影，他想知道最近的将来（可能发生在第二天）的某个时刻，使得镜像中的时钟时间是有效的。 可以证明，对于任意的 $h$、$m$、$s$，这样的时刻总是存在的。如果在居民开始观察时，镜像中的时间就是正确的，那么该时刻就被认为是最近的。 现在请你解决多个测试用例下的这个问题。

第一行包含一个整数 $T$（$1 \leq T \leq 100$）——表示测试用例的数量。 接下来的 $2 \cdot T$ 行描述每个测试用例。每个测试用例包含两行。 第一行包含两个整数 $h$、$m$（$1 \leq h, m \leq 100$）。 第二行包含一个起始时间 $s$，格式为 HH:MM。

对于每个测试用例，输出一行，表示最近的一个时刻（格式为 HH:MM），使得镜像中的时间是有效的。

在第二个测试用例中，不难发现 23:59 的镜像不是有效时间，而第二天的 00:00 的镜像是有效时间。  由 ChatGPT 4.1 翻译