CF1495D BFS Trees

我们定义图的生成树为以顶点 $s$ 为根的 BFS 树，当且仅当对于每个节点 $t$，图中 $s$ 到 $t$ 的最短距离等于生成树中 $s$ 到 $t$ 的最短距离。 给定一个图，我们定义 $f(x, y)$ 为该图中同时以 $x$ 和 $y$ 为根的 BFS 树的生成树数量。 给定一个无向连通图，包含 $n$ 个顶点和 $m$ 条边。请计算所有 $f(i, j)$，并对 $998\,244\,353$ 取模。

第一行包含两个整数 $n$ 和 $m$（$1 \le n \le 400$，$0 \le m \le 600$），分别表示图的顶点数和边数。 接下来的 $m$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \leq a_i, b_i \leq n$，$a_i < b_i$），表示一条连接 $a_i$ 和 $b_i$ 的无向边。 保证所有边均不相同，且图是连通的。

输出 $n$ 行，每行包含 $n$ 个整数。 第 $i$ 行第 $j$ 列输出 $f(i, j) \bmod 998\,244\,353$。

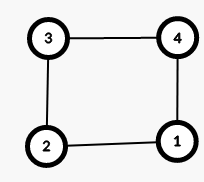
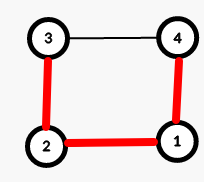
下图描述了第一个样例。  红色边组成的树是同时以 $1$ 和 $2$ 为根的 BFS 树。  类似地，其他相邻顶点对的 BFS 树也可以这样生成。 由 ChatGPT 4.1 翻译