CF1495F Squares

地板上从左到右画有 $n$ 个方格。第 $i$ 个方格上写有三个整数 $p_i, a_i, b_i$。序列 $p_1, p_2, \dots, p_n$ 构成一个排列。 每一轮你都从最左边的第 $1$ 个方格出发，向右跳跃。如果你现在在第 $i$ 个方格上，你可以进行以下两种操作之一： 1. 跳到第 $i+1$ 个方格，并支付代价 $a_i$。如果 $i=n$，则可以结束本轮并支付代价 $a_i$。 2. 跳到第 $j$ 个方格，并支付代价 $b_i$，其中 $j$ 是满足 $j>i$ 且 $p_j>p_i$ 的最左边的方格。如果不存在这样的 $j$，则可以结束本轮并支付代价 $b_i$。 游戏共有 $q$ 轮。为了增加难度，你需要维护一个方格集合 $S$（初始为空）。你必须在本轮经过集合 $S$ 中的所有方格（也可以经过其他方格）。第 $i$ 轮的集合 $S$ 是通过在第 $i-1$ 轮的集合基础上添加或移除一个方格得到的。 对于每一轮，求出你完成本轮所需支付的最小代价。

第一行包含两个整数 $n, q$（$1\le n, q\le 2 \cdot 10^5$）——方格数量和轮数。 第二行包含 $n$ 个互不相同的整数 $p_1, p_2, \dots, p_n$（$1\le p_i\le n$）。保证序列 $p_1, p_2, \dots, p_n$ 是一个排列。 第三行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$-10^9\le a_i\le 10^9$）。 第四行包含 $n$ 个整数 $b_1, b_2, \dots, b_n$（$-10^9\le b_i\le 10^9$）。 接下来 $q$ 行，每行包含一个整数 $x_i$（$1\le x_i\le n$）。如果 $x_i$ 在第 $i-1$ 轮的集合 $S$ 中，则将其移除，否则将其加入。

输出 $q$ 行，每行一个整数，表示完成对应轮所需支付的最小代价。

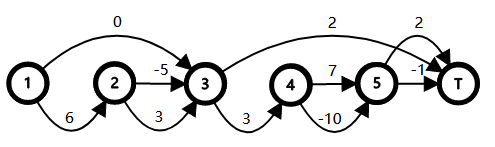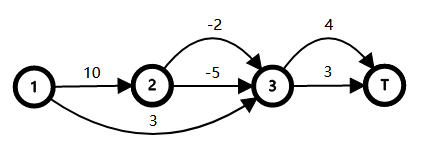
我们可以将字符 $T$ 视为一轮的结束。对于前两个测试，可以画出如下两张图。  在第一个测试的第一轮，必须经过的集合为 $\{1\}$。可行路径为 $1\to 3\to T$，总代价为 $6$。 在第一个测试的第二轮，必须经过的集合为 $\{1,2\}$。可行路径为 $1\to 2\to 3\to T$，总代价为 $8$。 由 ChatGPT 4.1 翻译