CF1498B Box Fitting

给定 $n$ 个矩形，每个矩形的高度为 $1$。每个矩形的宽度都是 $2$ 的幂（即可以表示为 $2^x$，其中 $x$ 是非负整数）。 还给定一个二维盒子，其宽度为 $W$。注意，$W$ 不一定是 $2$ 的幂。此外，$W$ 至少和所有矩形中最大的宽度一样大。 你需要求出该盒子的最小高度，使得能够放下所有给定的矩形。放置后盒子中可以有空余空间。 你不能旋转矩形来使其适应盒子。此外，任意两个不同的矩形不能重叠，即任意两个不同的矩形的交集面积必须为零。 具体样例的可视化说明见下方提示。

输入的第一行为一个整数 $t$（$1 \le t \le 5 \cdot 10^3$），表示测试用例的数量。每个测试用例包含两行。 对于每个测试用例： - 第一行包含两个整数 $n$（$1 \le n \le 10^5$）和 $W$（$1 \le W \le 10^9$）； - 第二行包含 $n$ 个整数 $w_1, w_2, \dots, w_n$（$1 \le w_i \le 10^6$），其中 $w_i$ 表示第 $i$ 个矩形的宽度。每个 $w_i$ 都是 $2$ 的幂； - 另外，保证 $\max\limits_{i=1}^{n} w_i \le W$。 所有测试用例中 $n$ 的总和不超过 $10^5$。

输出 $t$ 个整数。第 $i$ 个整数表示第 $i$ 个测试用例的答案——二维盒子的最小高度。

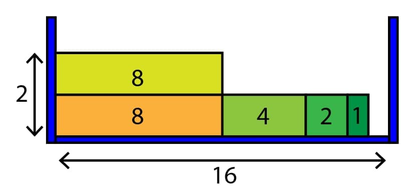
对于第一个样例，下面的图展示了一种将五个矩形以最小高度放入宽度为 $16$ 的二维盒子的方法：  在上图中，每个矩形内的数字表示其宽度。二维盒子的宽度为 $16$（下方箭头所示）。在这种情况下，二维盒子的最小高度为 $2$（左侧所示）。 对于第二个样例，你可以通过在每一层放置两个矩形（宽度分别为 $8$ 和 $2$），共三层，得到最小高度为 $3$。 由 ChatGPT 4.1 翻译